=============================================================
Manipulate[
{zmin, zmax} = Evaluate@Switch[f,
Function[{x1, y1}, Sin[x1 - y1] + Cos[x1]], {-2, 2},
Function[{x1, y1}, x1*Cos[y1]], {-3, 3},
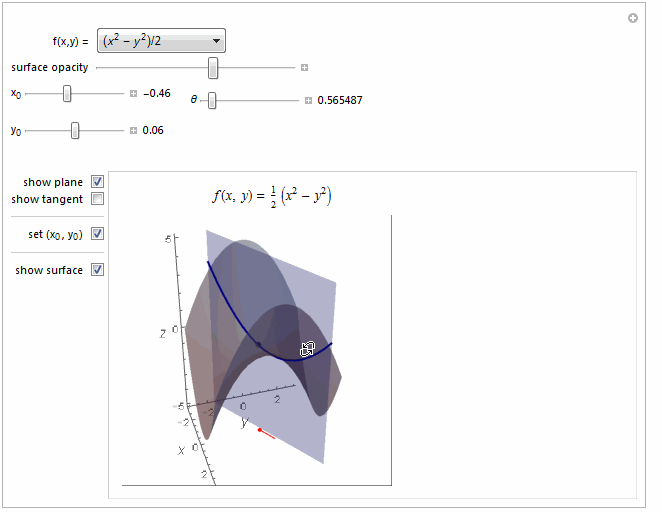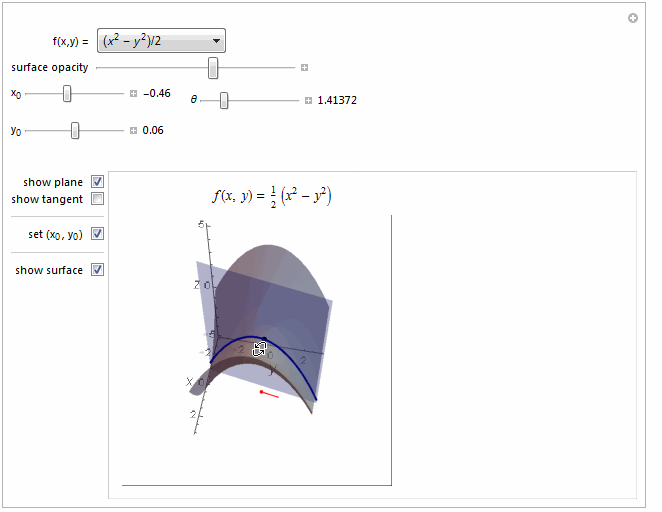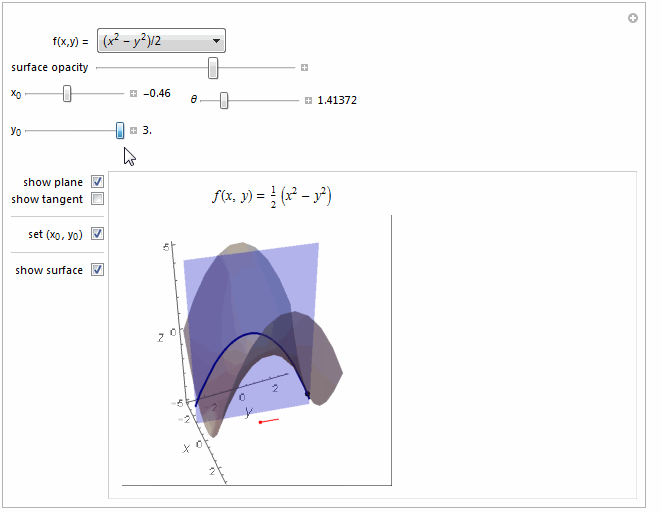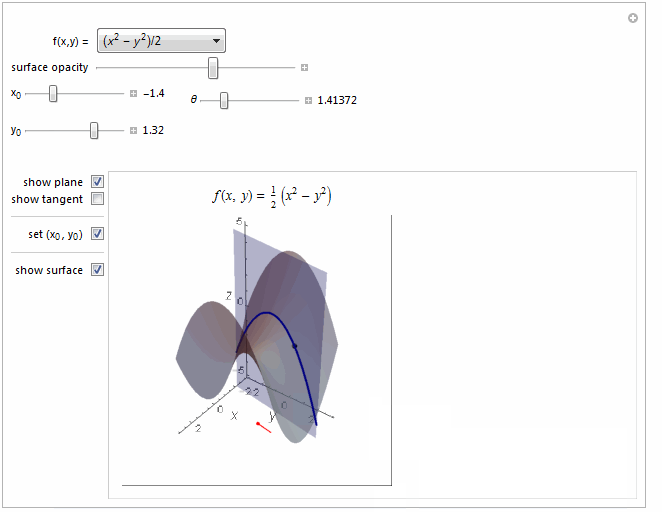
Function[{x1, y1}, (x1^2 - y1^2)/2], {-5, 5},
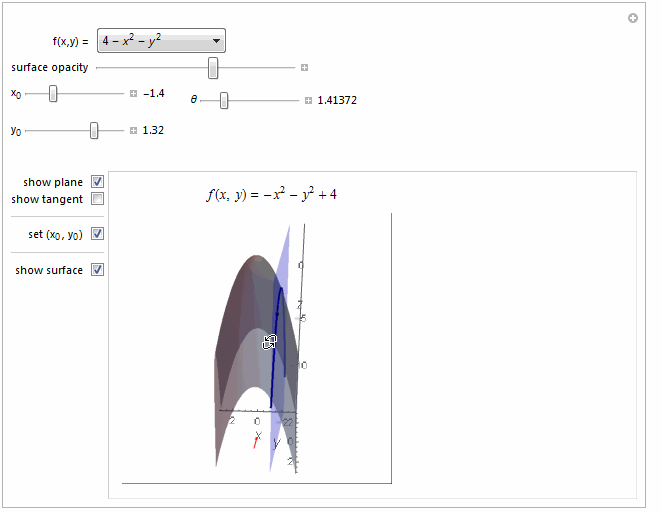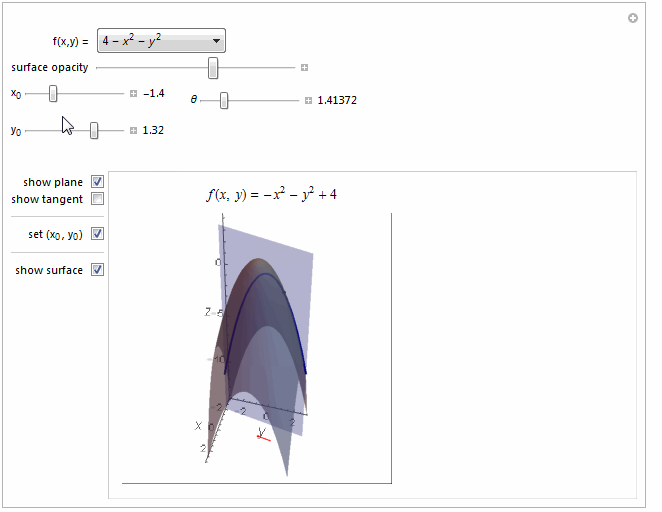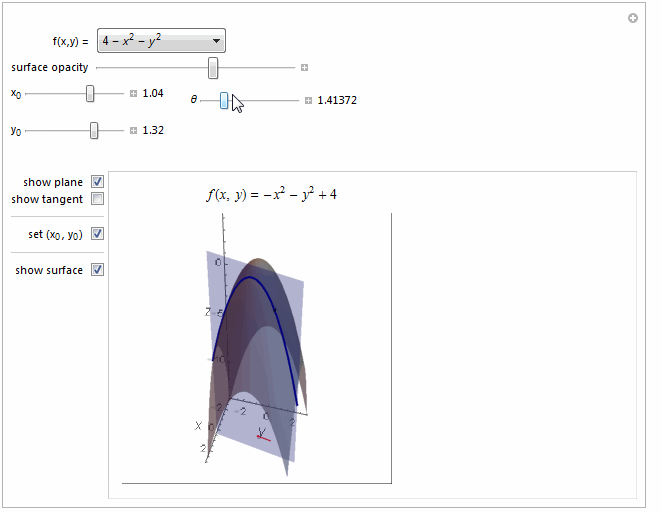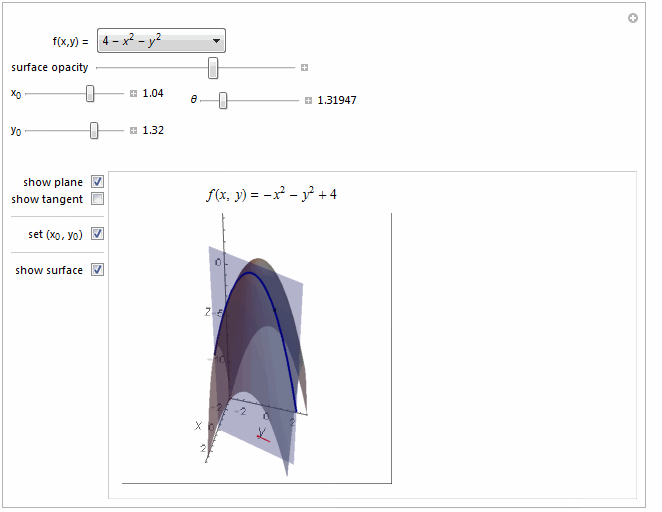
Function[{x1, y1}, 4 - x1^2 - y1^2], {-14, 4}
];
plotrange = {{xmin, xmax}, {ymin, ymax}, {zmin, zmax}};
(*plotrange=AbsoluteOptions[Plot3D[f[x,y],{x,xmin,xmax},{y,ymin,ymax}\
],PlotRange];*)
Pane[
Grid[{
{
If[setxy, pt = {x0, y0}, {x0, y0} = pt];
{a, b} = {Cos[theta], Sin[theta]};
slope = ({D[f[x, y], x], D[f[x, y], y]}.{a, b} /. {x ->
a*t0 + x0, y -> b*t0 + y0});
Grid[{{Text@
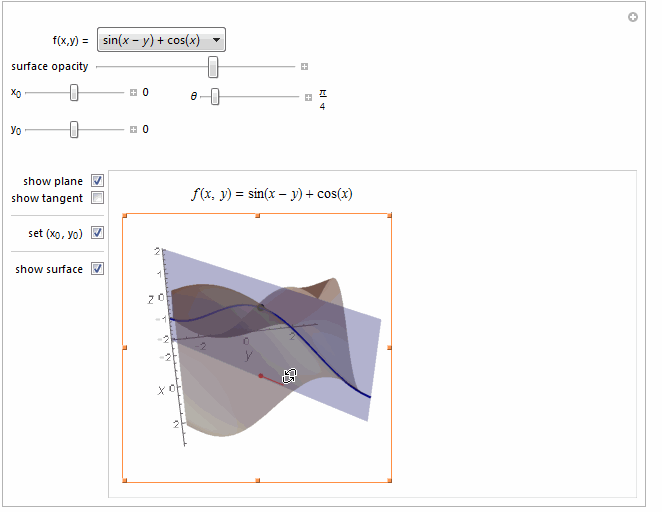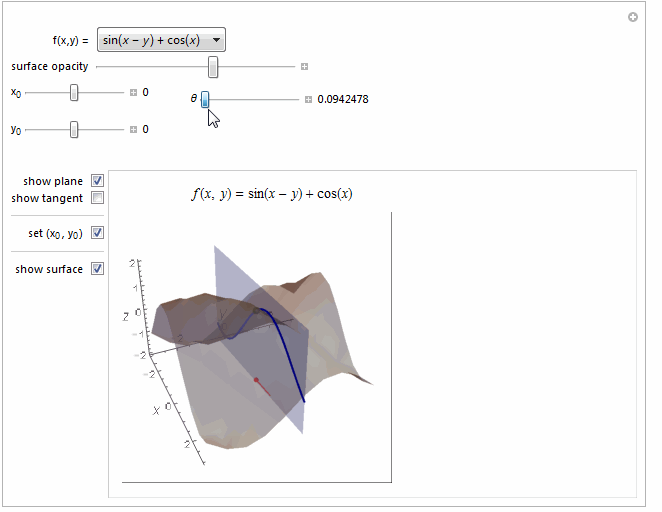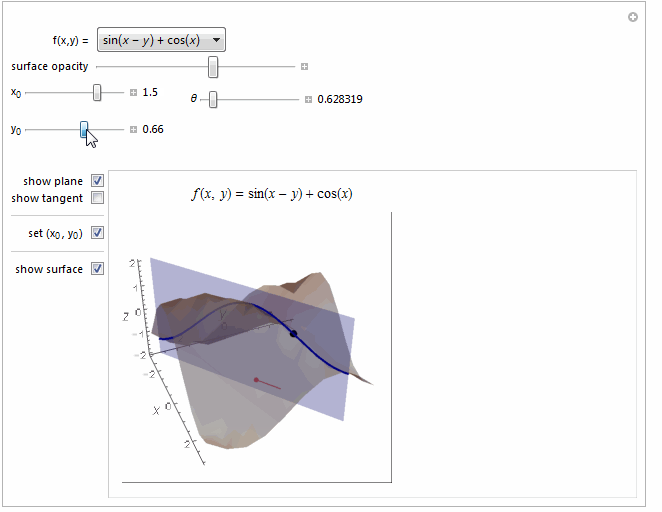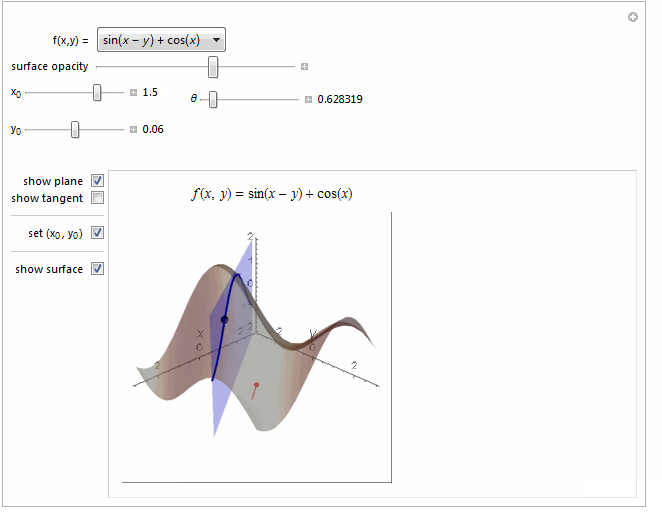
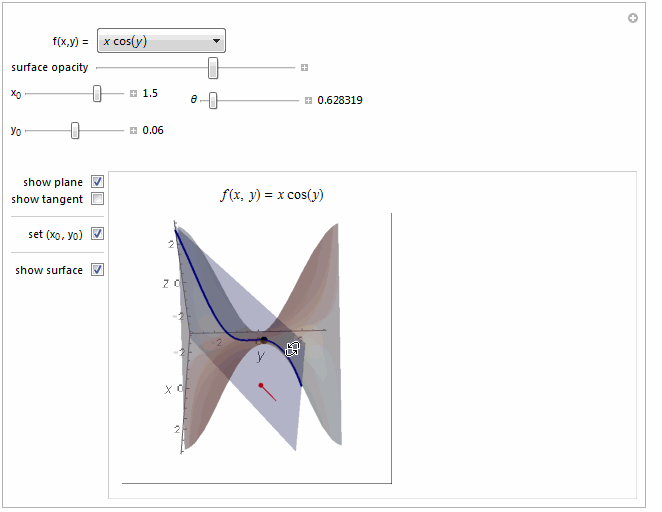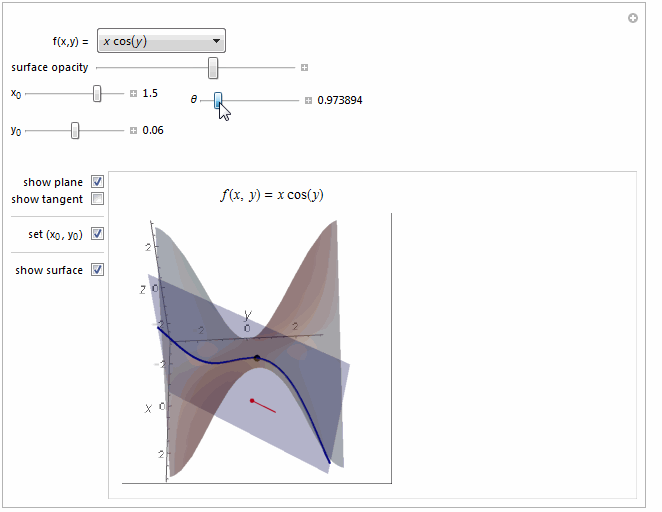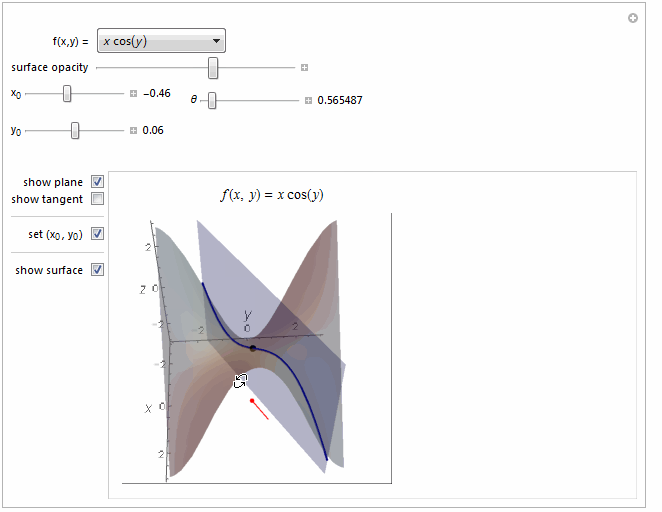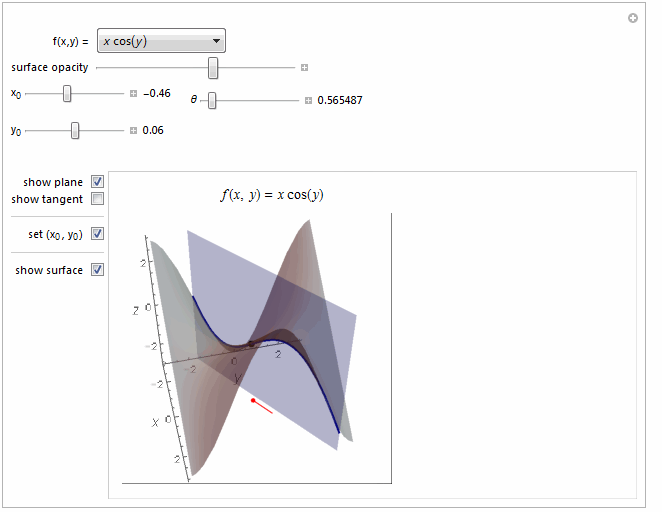
Style[Row[{Style["f", Italic], "(", Style["x", Italic], ", ",
Style["y", Italic], ") = ", TraditionalForm[f[x, y]]}],
14]}}, ItemSize -> {Automatic, 2.2}, Alignment -> Top],
SpanFromLeft},
{
Item[Show[
If[showsurf,
Plot3D[f[x, y], {x, xmin, xmax}, {y, ymin, ymax},
Mesh -> False, PlotStyle -> {Gray, Opacity[surfopac]},
BoundaryStyle -> None], {}],
If[showplane,
ParametricPlot3D[{a*t + x0, b*t + y0,
f[a*t + x0, b*t + y0]}, {t, -10, 10},
PlotStyle -> {Thick, Darker[Blue, 0.5]}], {}],
If[showderiv, ParametricPlot3D[
{a*t, b*t,
slope*t} + {a*t0 + x0, b*t0 + y0, f[a*t0 + x0, b*t0 + y0]},
{t, -1, 1}, PlotStyle -> {Blue, Thick}], {}],
Graphics3D[{
{Red, PointSize[0.02],
Point[{0, 0, plotrange[[3, 1]]}]}, {Red,
Line[{{0, 0, plotrange[[3, 1]]}, {a, b,
plotrange[[3, 1]]}}]},
{Black, PointSize[0.01], Point[{{x0, y0, f[x0, y0]}}]},
If[
showderiv, {Darker[Blue, 0.5], PointSize[0.03],
Point[{{a*t0 + x0, b*t0 + y0,
f[a*t0 + x0, b*t0 + y0]}}]}, {Black, PointSize[0.03],
Point[{{x0, y0, f[x0, y0]}}]}],
If[showplane, {Blue, Opacity[0.3],
Polygon[{{-100 a + x0, -100 b + y0, -100}, {100 a + x0,
100 b + y0, -100}, {100 a + x0, 100 b + y0,
100}, {-100 a + x0, -100 b + y0, 100}}]}, {}]
}],
Boxed -> False, Axes -> True, AxesEdge -> Table[-1, {3}, {2}],
BoxRatios -> Automatic, PlotRange -> plotrange,
ImageSize -> {275, 275},
AxesLabel ->
Map[Style[#, 14] &, {Style["x", Italic], Style["y", Italic],
Style["z", Italic]}]
], Alignment -> Top],
" ",
Text@Item[Style[Column[{
"",
If[showderiv, Style[Column[{
Row[{Subscript[Style["D", Italic], u],
Style["f", Italic], "(", Style["x", Italic], ", ",
Style["y", Italic], ") = \[Del]", Style["f", Italic],
"(", Style["x", Italic], ", ", Style["y", Italic],
") ", Style["\[CenterDot]", Bold, 14],
Style[" u", Italic]}],
Row[{"\[Del]", Style["f", Italic], "(",
Style["x", Italic], ", ", Style["y", Italic], ") = (",
Subscript[Style["f", Italic], x], ", ",
Subscript[Style["f", Italic], y], ")"}],
"",
Row[{Subscript[Style["f", Italic], x], "(",
Style["x", Italic], ", ", Style["y", Italic], ") = ",
TraditionalForm@D[f[x, y], x]}],
Row[{Subscript[Style["f", Italic], x], "(",
rndif[a*t0 + x0], ", ", rndif[b*t0 + y0], ") = ",
D[f[x, y], x] /. {x -> x0, y -> y0}}],
"",
Row[{Subscript[Style["f", Italic], y], "(",
Style["x", Italic], ", ", Style["y", Italic], ") = ",
TraditionalForm@D[f[x, y], y]}],
Row[{Subscript[Style["f", Italic], y], "(",
rndif[a*t0 + x0], ", ", rndif[b*t0 + y0], ") = ",
TraditionalForm@D[f[x, y], y] /. {x -> x0, y -> y0}}],
"",
Row[{"u = (", rndif[a], ", ", rndif[b], ")"}],
"",
Row[{Subscript["D", u], Style["f", Italic], "(",
rndif[a*t0 + x0], ", ", rndif[b*t0 + y0], ") = ",
TraditionalForm[slope]}]
}], Blue], ""]
}], 12], ItemSize -> 15.8, Alignment -> Left]
}}, Alignment -> Top, ItemSize -> {Automatic, Automatic}],
{500, 300}],
{{f, Function[{x1, y1}, Sin[x1 - y1] + Cos[x1]], "f(x,y) ="}, {
Function[{x1, y1}, Sin[x1 - y1] + Cos[x1]] ->
Row[{"sin(", Style["x", Italic], " - ", Style["y", Italic],
") + cos(", Style["x", Italic], ")"}],
Function[{x1, y1}, x1*Cos[y1]] ->
Row[{Style["x", Italic], " cos(", Style["y", Italic], ")"}],
Function[{x1, y1}, (x1^2 - y1^2)/2] ->
Row[{"(", Superscript[Style["x", Italic], 2], " - ",
Superscript[Style["y", Italic], 2], ")/2"}],
Function[{x1, y1}, 4 - x1^2 - y1^2] ->
Row[{"4 - ", Superscript[Style["x", Italic], 2], " - ",
Superscript[Style["y", Italic], 2]}]
},
PopupMenu}
,
{{surfopac, 0.5, "surface opacity"}, 0, 1},
Row[{
PaneSelector[
{True ->
Column[{
Row[{Subscript["x", 0], " ",
Manipulator[Dynamic[x0], {-3, 3}, ImageSize -> Small,
Appearance -> "Labeled"]}], "",
Row[{Subscript["y", 0], " ",
Manipulator[Dynamic[y0], {-3, 3}, ImageSize -> Small,
Appearance -> "Labeled"]}]
}],
False ->
Row[{"(", Subscript["x", 0], ", ", Subscript["y", 0], ") = ",
Slider2D[Dynamic[pt], {{-3, -3}, {3, 3}}]}]},
Dynamic@setxy
],
" ",
Column[{Row[{"\[Theta] ",
Manipulator[Dynamic[theta], {0, 2 Pi}, Appearance -> "Labeled",
ImageSize -> Small]}],
PaneSelector[{True ->
Row[{"slide tangent ",
Manipulator[Dynamic[t0, {(t0 = #) &, (t0 = 0) &}], {-3, 3},
ImageSize -> Small]}], False -> ""},
Dynamic@showderiv]}, Alignment -> Left]}],
{{pt, {Mean[{xmin, xmax}], Mean[{ymin, ymax}]},
Row[{"(", Subscript["x", 0], ", ", Subscript["y", 0],
") = "}]}, {xmin, ymin}, {xmax, ymax}, None},
{{theta, Pi/4, "\[Theta]"}, 0, 2 Pi, None},
{{t0, 0, Subscript["t", 0]}, -3, 3, None},
{{showplane, True, "show plane"}, {True, False},
ControlPlacement -> Left},
{{showderiv, False, "show tangent"}, {True, False},
ControlPlacement -> Left},
Delimiter,
{{setxy, False,
Row[{"set (", Subscript["x", 0], ", ", Subscript["y", 0],
")"}]}, {True, False}, ControlPlacement -> Left},
Delimiter,
{{showsurf, True, "show surface"}, {True, False},
ControlPlacement -> Left},
{{x0, 0}, ControlType -> None},
{{y0, 0}, ControlType -> None},
Initialization :> (rndif[x_] :=
If[Accuracy[x] == Infinity, x, Round[x, 0.001]];
{{xmin, xmax}, {ymin, ymax}} = {{-3, 3}, {-3, 3}};),
AutorunSequencing -> {1, 2, 3, 4, 7}, TrackedSymbols -> Manipulate
]
|
