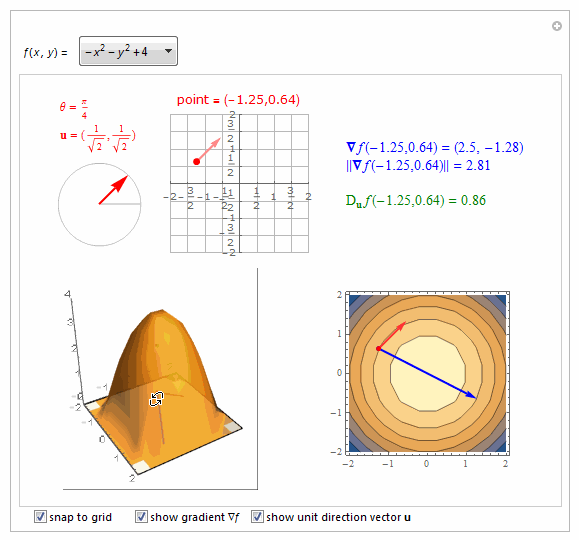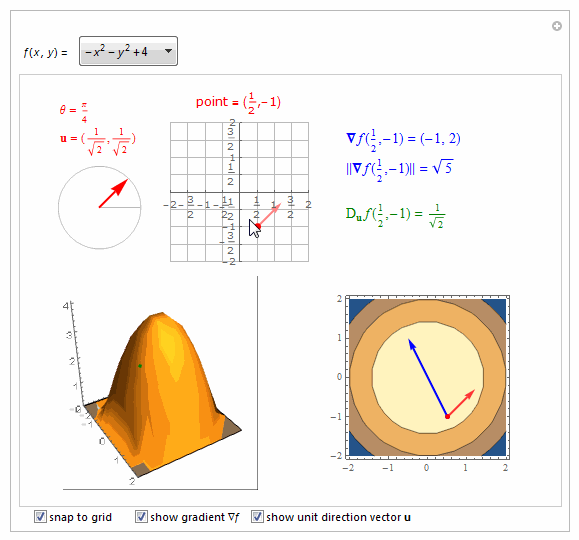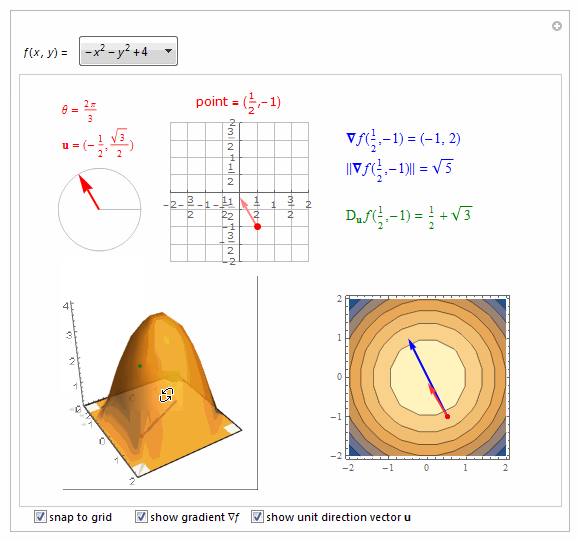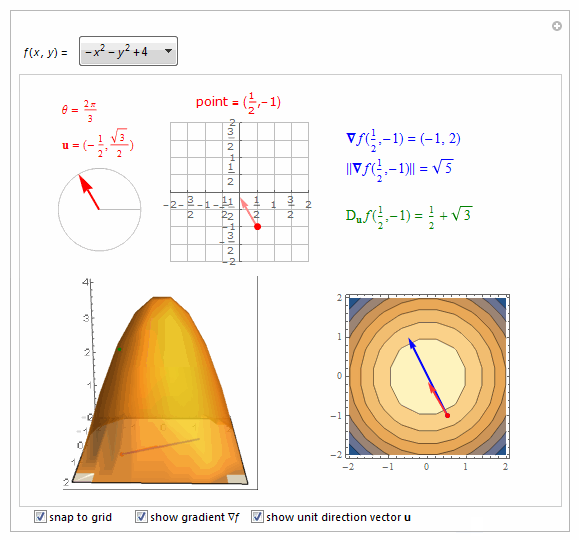
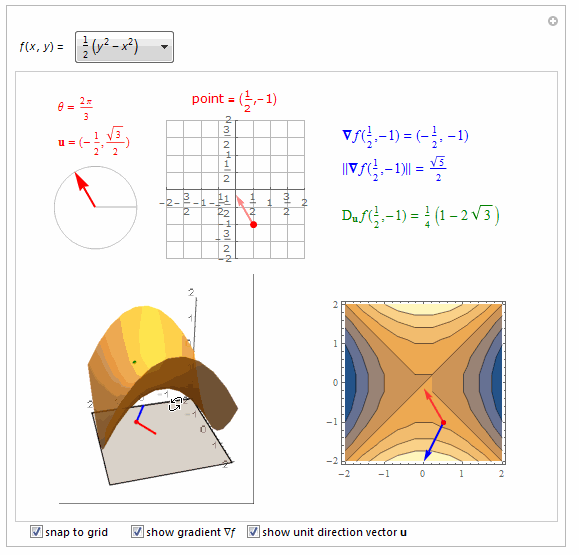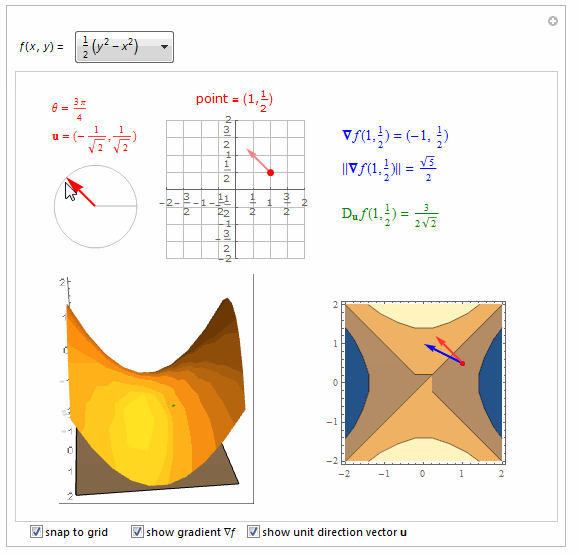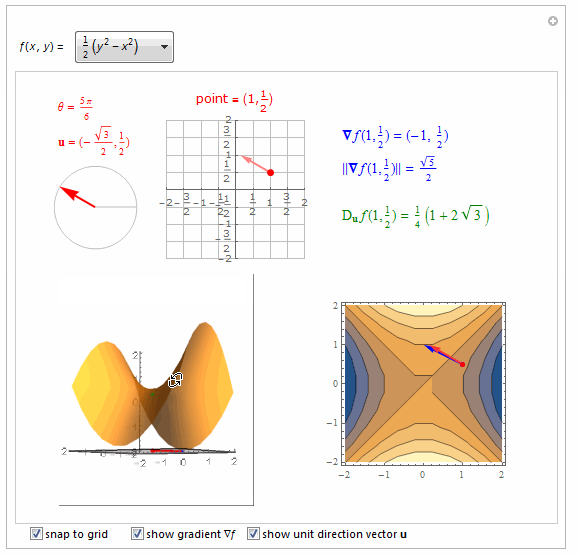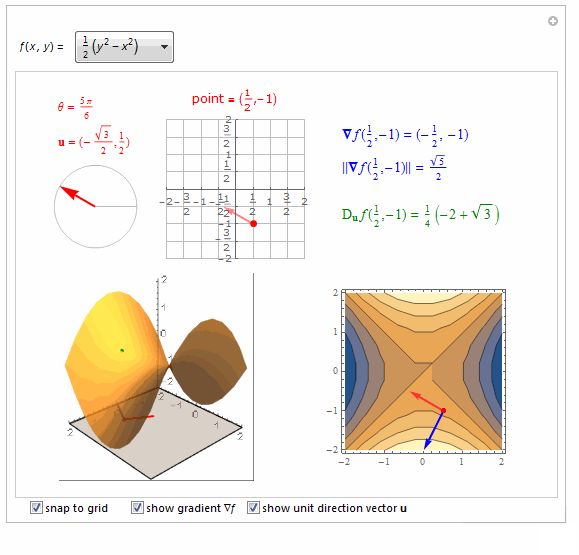
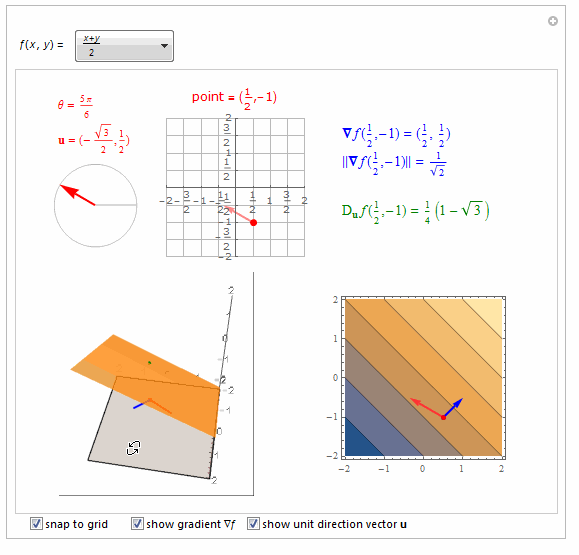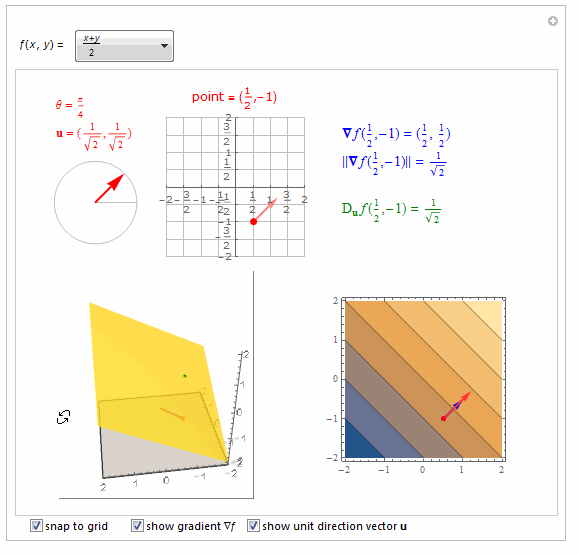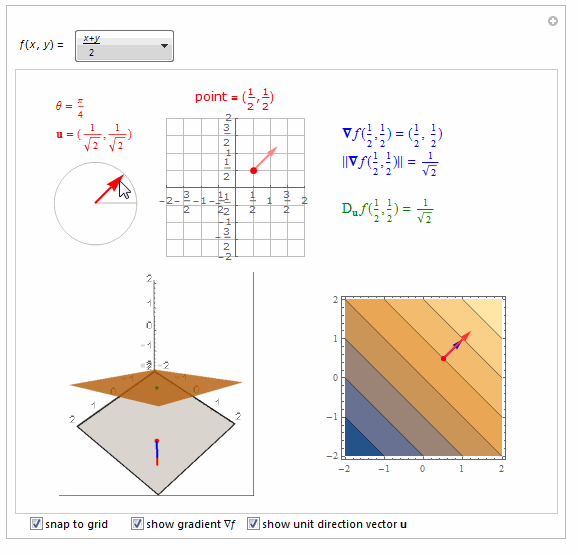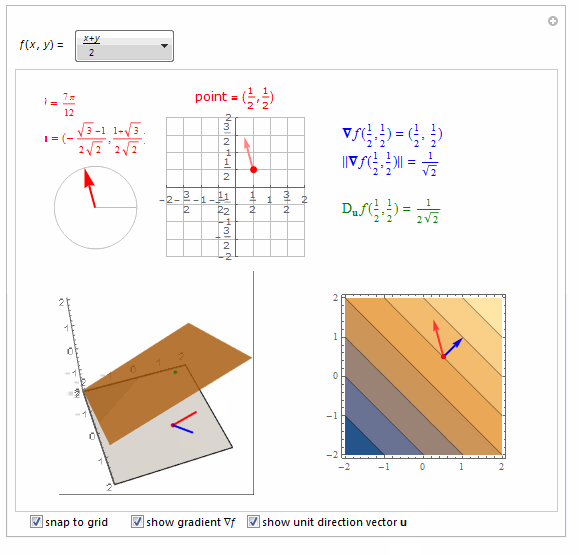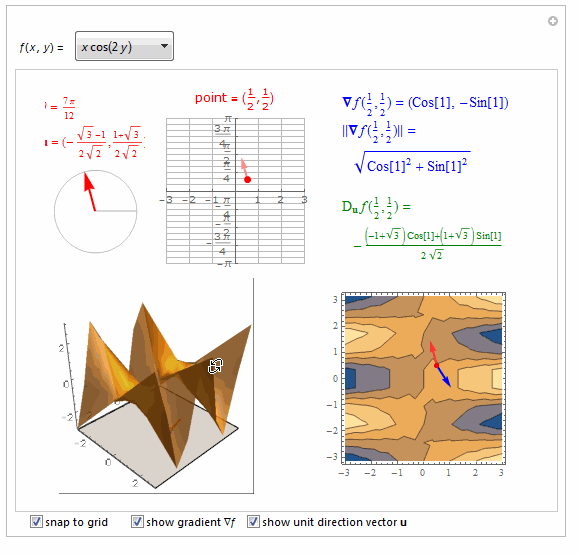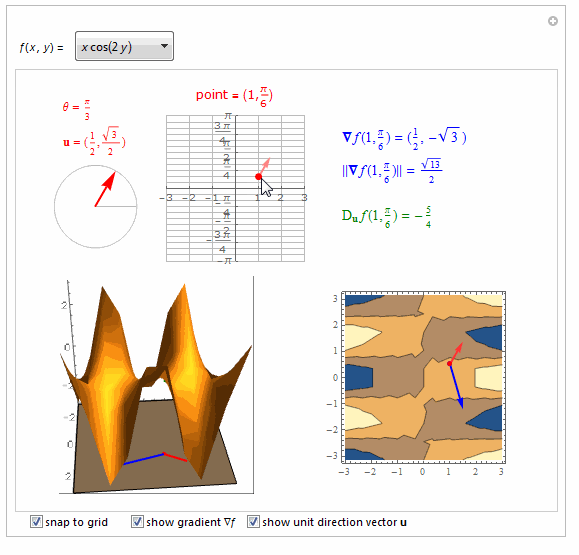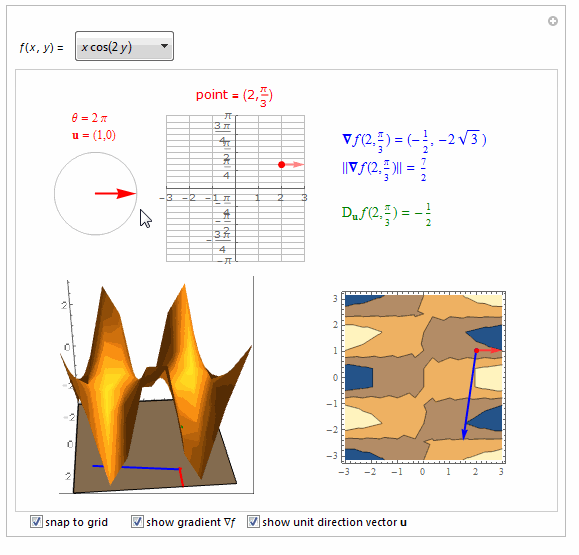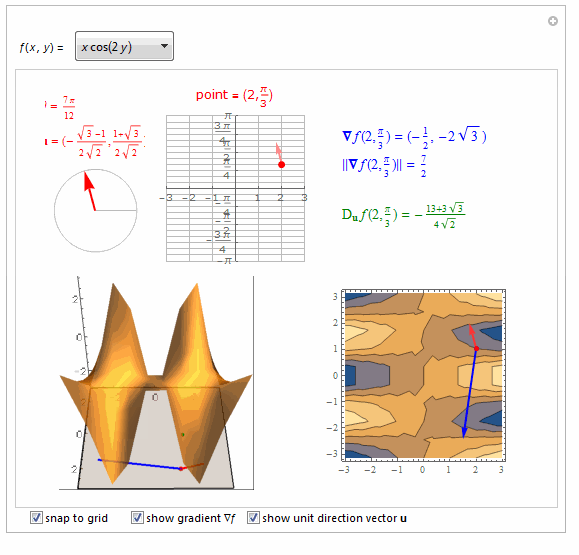
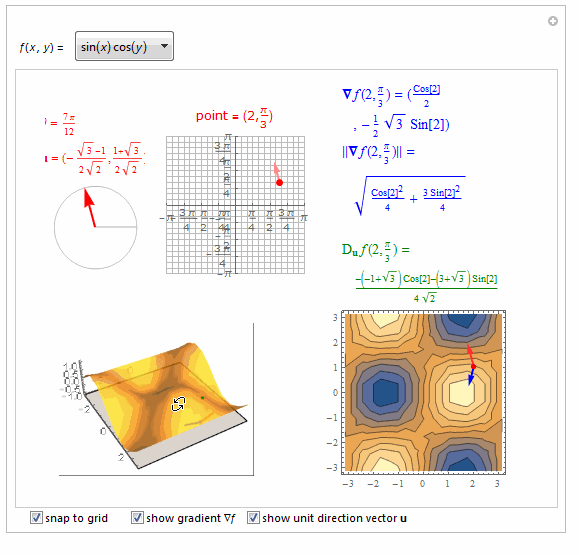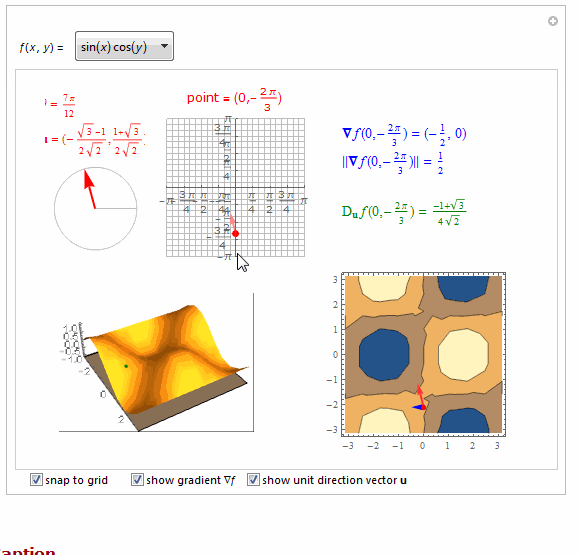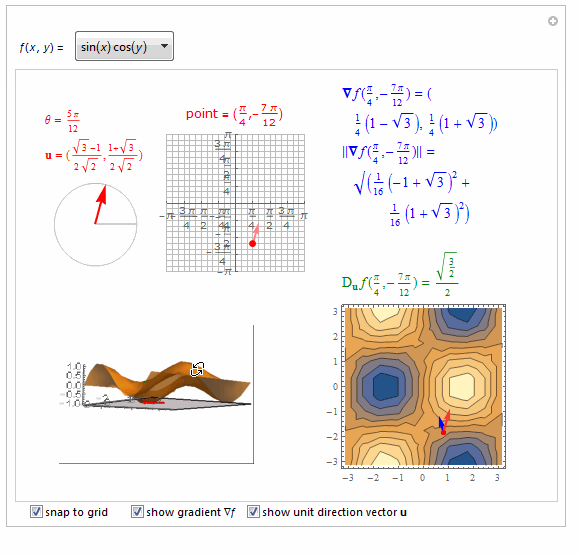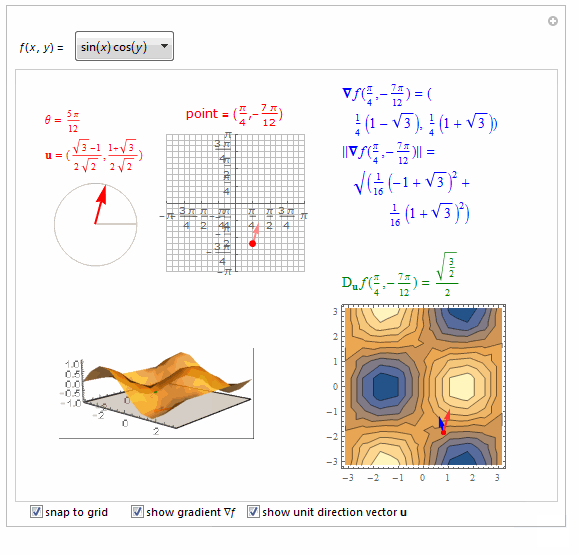
===============================================================

Manipulate[
 
 rnd[x_] := If[Accuracy[x] == Infinity, x, Round[x, 0.01]];
 pitest[x_] := Or[Head[x/Pi] === Integer, Head[x/Pi] === Rational];
 
 DynamicModule[{surfacegraph, anglegraph, contourgraph, pointgraph, 
   ff , xmin, xmax, ymin, ymax, zmin, zmax, xgrid1, ygrid1, 
   thept = ptctrl, angpt = {Cos[angctrl], Sin[angctrl]}, 
   ang = angctrl},
  
  Switch[fcn,
   f1,
   ff[x_, y_] := 4 - x^2 - y^2;
   xmin = -2; xmax = 2; ymin = -2; ymax = 2; zmin = 0; zmax = 4.1;
   {xgrid1, ygrid1} = {1/2, 1/2},
   f2,
   ff[x_, y_] := (y^2 - x^2)/2;
   xmin = -2; xmax = 2; ymin = -2; ymax = 2; zmin = -2.1; zmax = 2.1;
   {xgrid1, ygrid1} = {1/2, 1/2},
   f3,
   ff[x_, y_] := x Cos[2 y];
   xmin = -3; xmax = 3; ymin = -Pi; ymax = Pi; zmin = -3.1; zmax = 3.1;
   {xgrid1, ygrid1} = {1, Pi/12},
   f4,
   ff[x_, y_] := Sin[x] Cos[y];
   xmin = -Pi; xmax = Pi; ymin = -Pi; ymax = Pi; zmin = -1.1; 
   zmax = 1.1;
   {xgrid1, ygrid1} = {Pi/12, Pi/12},
   f5,
   ff[x_, y_] := (x + y)/2;
   xmin = -2; xmax = 2; ymin = -2; ymax = 2; zmin = -2.1; zmax = 2.1;
   {xgrid1, ygrid1} = {1/2, 1/2}
   ];
  {xgrid, ygrid} = 
   If[MemberQ[opts, gridsnap], {xgrid1, ygrid1}, {0.001, 0.001}];
  
  surfacegraph[thept_, angpt_] :=
   Show[
    Plot3D[ff[x, y], {x, xmin, xmax}, {y, ymin, ymax}, 
     PlotStyle -> Opacity[ControlActive[1, 0.8]], Mesh -> False, 
     PlotRange -> {{xmin, xmax}, {ymin, ymax}, {zmin, zmax}}, 
     PerformanceGoal -> "Speed"],
    Graphics3D[{{Darker[Green, 0.5], PointSize[0.02], 
       Point[{thept[[1]], thept[[2]], ff[thept[[1]], thept[[2]]]}]},
      If[MemberQ[opts, 
        showgrad], {{Blue, Thick, 
         Line[{{thept[[1]], thept[[2]], zmin}, 
           Append[thept + D[ff[x, y], {{x, y}}] /. {x -> thept[[1]], 
              y -> thept[[2]]}, zmin]}]},
        {Blue, PointSize[0.025], 
         Point[{thept[[1]], thept[[2]], zmin}]}}, {}], 
      If[MemberQ[opts, showunit],
       {{Red, PointSize[0.025], 
         Point[{thept[[1]], thept[[2]], zmin}]}, {Red, Thick, 
         Line[{{thept[[1]], thept[[2]], 
            zmin}, {thept[[1]] + angpt[[1]], thept[[2]] + angpt[[2]], 
            zmin}}]}}, {}],
      {Gray, Opacity[ControlActive[1, 0.3]], 
       Polygon[{{xmin, ymin, zmin}, {xmin, ymax, zmin}, {xmax, ymax, 
          zmin}, {xmax, ymin, zmin}}]}
      }],
    ParametricPlot3D[{angpt[[1]] t + thept[[1]], 
      angpt[[2]] t + 
       thept[[2]], (D[ff[x, y], {{x, y}}].angpt /. {x -> thept[[1]], 
           y -> thept[[2]]}) t + f[thept[[1]], thept[[2]]]}, {t, -1, 
      1}, PlotStyle -> Darker[Green, 0.5], MaxRecursion -> 0, 
     PerformanceGoal -> "Speed"],
    AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, ImageSize -> 195, 
    BoxRatios -> {xmax - xmin, ymax - ymin, zmax - zmin}, 
    PlotRange -> {{xmin, xmax}, {ymin, ymax}, {zmin, zmax}}, 
    Boxed -> False
    ];
  
  anglegraph[angpt_, opts___] := 
   Graphics[{{Lighter[Gray, 0.5], 
      Circle[{0, 0}, 1]}, {Lighter[Gray, 0.5], Line[{{0, 0}, {1, 0}}]},
     {Red, Thick, Arrowheads[Large], Arrow[{{0, 0}, angpt}]}}, 
    PlotRange -> 1.2, ImageSize -> 100, opts];
  
  contourgraph[thept_, angpt_] := 
   Show[ContourPlot[ff[x, y], {x, xmin, xmax}, {y, ymin, ymax}, 
     Contours -> ControlActive[3, Automatic], 
     FrameTicks -> {Table[
        n, {n, xmin, xmax, If[pitest[xgrid1], 3 xgrid1, xgrid1]}], 
       Table[n, {n, ymin, ymax, 
         If[pitest[ygrid1], 3 ygrid1, ygrid1]}], True, True}, 
     PerformanceGoal -> "Speed"],
    Graphics[{
      If[MemberQ[opts, 
        showgrad], {{Blue, PointSize[0.03], Point[thept]}, {Blue, 
         Thick, Arrowheads[Medium], 
         Arrow[{thept, 
           thept + D[ff[x, y], {{x, y}}] /. {x -> thept[[1]], 
             y -> thept[[2]]}}]}}, {}], 
      If[MemberQ[opts, 
        showunit], {{Lighter[Red, 0.2], Thick, Arrowheads[Medium], 
         Arrow[{thept, thept + angpt}]}, {Red, PointSize[0.03], 
         Point[thept]}}, {}]}], ImageSize -> 180, 
    AspectRatio -> Automatic];
  
  pointgraph[thept_, angpt_, opts___] := 
   Graphics[{{Lighter[Red, 0.5], Thick, Arrowheads[Medium], 
      Arrow[{thept, thept + angpt}]}, {Red, PointSize[0.05], 
      Point[thept]}}, Axes -> True, 
    PlotRange -> {{xmin, xmax}, {ymin, ymax}}, 
    AspectRatio -> Automatic, opts, 
    GridLines -> {Table[{n, Lighter[Gray, 0.5]}, {n, xmin, xmax, 
        xgrid1}], 
      Table[{n, Lighter[Gray, 0.5]}, {n, ymin, ymax, ygrid1}]},
    Ticks -> {Table[
       n, {n, xmin, xmax, If[pitest[xgrid1], 3 xgrid1, xgrid1]}], 
      Table[n, {n, ymin, ymax, 
        If[pitest[ygrid1], 3 ygrid1, ygrid1]}]}, 
    BaseStyle -> {10, "Label"}, ImageSize -> 150];
  
  Column[{
    Grid[{
      {Grid[{{Deploy@LocatorPane[Dynamic[angpt,
             {(angpt = {Cos[angctrl], Sin[angctrl]}) &,
              (ang = 
                 If[MemberQ[opts, gridsnap], 
                  Round[Mod[ArcTan[#[[1]], #[[2]]], 2 Pi], Pi/12], 
                  Mod[ArcTan[#[[1]], #[[2]]], 2 Pi]];
                angpt = Normalize[{Cos[ang], Sin[ang]}]) &,
              (angpt = Normalize[{Cos[ang], Sin[ang]}]; 
                angctrl = 
                 Mod[ArcTan[angpt[[1]], angpt[[2]]], 2 Pi]) &}], 
            Dynamic[
             anglegraph[angpt, 
              PlotLabel -> 
               Column[{Style[Row[{"\[Theta] = ", Simplify[rnd@ang]}], 
                  Red], Style[
                  Row[{Style["u", Bold], " = (", 
                    Simplify[rnd@angpt[[1]]], ",", 
                    Simplify[rnd@angpt[[2]]], ")"}], Red]}]]], 
            Appearance -> None],
          
          Deploy@LocatorPane[Dynamic[thept,
             {thept = ptctrl,
              (thept = 
                 If[MemberQ[opts, gridsnap], 
                  Round[#, {xgrid, ygrid}], #]) &,
              (thept = 
                 If[MemberQ[opts, gridsnap], 
                  Round[#, {xgrid, ygrid}], #]; 
                ptctrl = 
                 If[MemberQ[opts, gridsnap], 
                  Round[#, {xgrid, ygrid}], #]) &}],
            
            Dynamic[
             pointgraph[thept, angpt, 
              PlotLabel -> 
               Style[Row[{"point = (", rnd@thept[[1]], ",", 
                  rnd@thept[[2]], ")"}], Red]]], Appearance -> None],
          "  ",
          Column[{
            Deploy@Dynamic[Text[Column[Style[#, 14] & /@ {
                  
                  Style[Row[{Style["\[Del]", Bold], TraditionalForm@f,
                     "(", rnd@thept[[1]], ",", rnd@thept[[2]], ") = ",
                     "(", (rnd[
                    D[ff[x, y], {{x, y}}] /. {x -> thept[[1]], 
                    y -> thept[[2]]}])[[1]], 
                    ", ", (rnd[
                    D[ff[x, y], {{x, y}}] /. {x -> thept[[1]], 
                    y -> thept[[2]]}])[[2]], ")"}], Blue],
                  
                  Style[Row[{"||", Style["\[Del]", Bold], 
                    TraditionalForm@f, "(", rnd@thept[[1]], ",", 
                    rnd@thept[[2]], ")|| = ", 
                    rnd[Norm[
                    D[ff[x, y], {{x, y}}] /. {x -> thept[[1]], 
                    y -> thept[[2]]}]]}], Blue],
                  "",
                  
                  Style[Row[{Subscript["D", Style["u", Bold]], 
                    TraditionalForm@f, "(", thept[[1]], ",", 
                    thept[[2]], ") = ", 
                    Simplify@
                    rnd[D[ff[x, y], {{x, y}}].angpt /. {x -> 
                    thept[[1]], y -> thept[[2]]}]}], 
                   Darker[Green, 0.5]]
                  }]]]
            }, ItemSize -> {"Columns" -> {15, 20, 5, 10}}, 
           Alignment -> Left]}}],
       
       SpanFromLeft},
      
      {Dynamic[surfacegraph[thept, angpt]],
       
       Deploy@Dynamic[contourgraph[thept, angpt]]}
      }, ItemSize -> {20}]
    
    }, Alignment -> {Center, Top}, ItemSize -> {"Rows" -> {20, 6}}]
  
  ] (*End Module*),
 
 {{fcn, f1, 
   Row[{TraditionalForm[f[x, y]], " = "}]}, {f1 -> 
    TraditionalForm[4 - x^2 - y^2], 
   f2 -> TraditionalForm[(y^2 - x^2)/2], 
   f5 -> TraditionalForm[(x + y)/2], 
   f3 -> TraditionalForm[x Cos[2 y]], 
   f4 -> TraditionalForm[Sin[x] Cos[y]]}, ControlType -> PopupMenu},
 {{opts, {showgrad, showunit}, ""}, {gridsnap -> "snap to grid     ", 
   showgrad -> Row[{"show gradient \[Del]", TraditionalForm@f, " "}], 
   showunit -> Row[{"show unit direction vector ", Style[u, Bold]}]}, 
  ControlType -> CheckboxBar, ControlPlacement -> Bottom},
 {{ptctrl, {(xmin + xmax)/2, (ymin + ymax)/2}}, {xmin, ymin}, {xmax, 
   ymax}, ControlType -> None},
 {{angctrl, Pi/4}, 0, 2 Pi, ControlType -> None},
 
 TrackedSymbols :> {fcn, ptctrl, angctrl, opts},
 Initialization :> {
   xmin = -2; xmax = 2; ymin = -2; ymax = 2; zmin = 0; zmax = 4.1;
   {xgrid1, ygrid1} = {1/2, 1/2}
   }
 ]