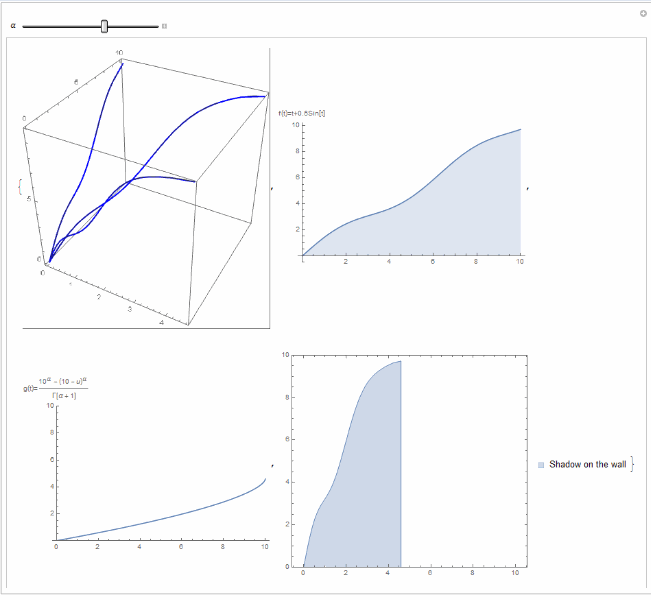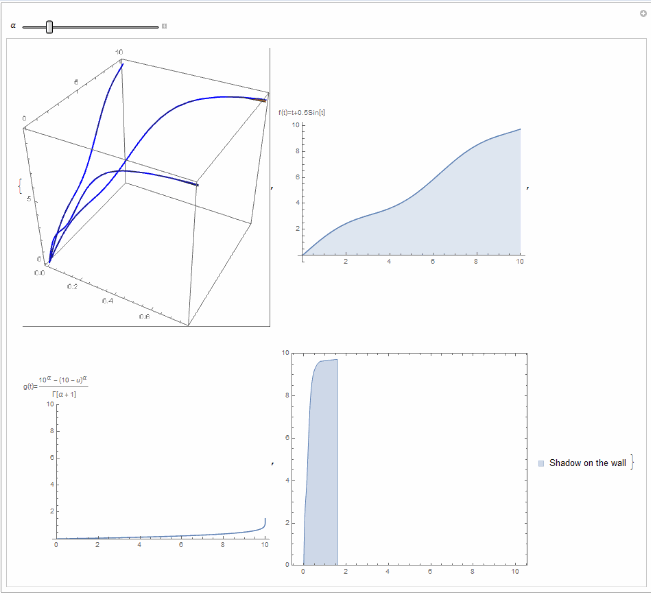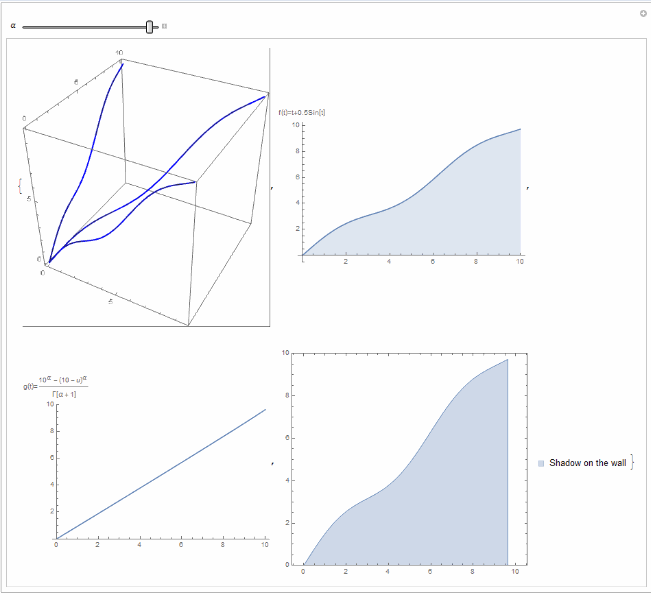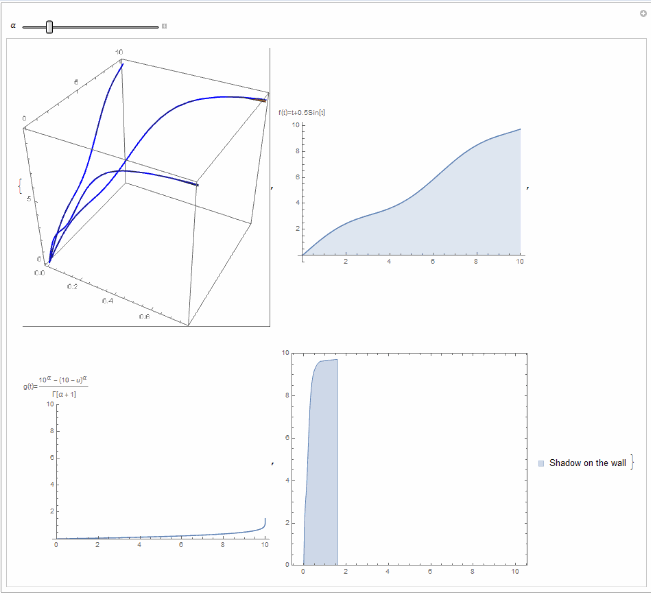
============================================================= 

Manipulate[{ParametricPlot3D[{{(10^\[Alpha] - (10 - u)^\[Alpha])/
     Gamma[\[Alpha] + 1], u, u + 0.5*Sin[u]}, {(
     10^\[Alpha] - (10 - u)^\[Alpha])/Gamma[\[Alpha] + 1], 0, 
     u + 0.5*Sin[u]}, {0, u, u + 0.5*Sin[u]}}, {t, 0, 10}, {u, 0, 10},
    BoxRatios -> {1, 1, 1}, BoundaryStyle -> Directive[Blue, Thick]], 
  Plot[u + 0.5*Sin[u], {u, 0, 10}, Filling -> Bottom, 
   AxesLabel -> "f(t)=t+0.5Sin[t]"], 
  Plot[(10^\[Alpha] - (10 - u)^\[Alpha])/
   Gamma[\[Alpha] + 1], {u, 0, 10}, PlotRange -> {0, 10}, 
   AxesLabel -> 
    "g(t)=\!\(\*FractionBox[\(\*SuperscriptBox[\(10\), \(\[Alpha]\)] \
- \*SuperscriptBox[\((10 - u)\), \(\[Alpha]\)]\), \(\(\\\ \)\(\
\[CapitalGamma][\[Alpha] + 1]\)\)]\)"], 
  ParametricPlot[{(10^\[Alpha] - (10 - u)^\[Alpha])/
    Gamma[\[Alpha] + 1], m*(u + 0.5*Sin[u])}, {u, 0, 10}, {m, 0, 1}, 
   PlotRange -> {0, 10}, 
   PlotLegends -> {"Shadow on the wall"}]}, {\[Alpha], 0, 1}]