.

===========================================================

code:

Manipulate[
 DynamicModule[{grad, unitgrad, function, buttonText, functionButtons},
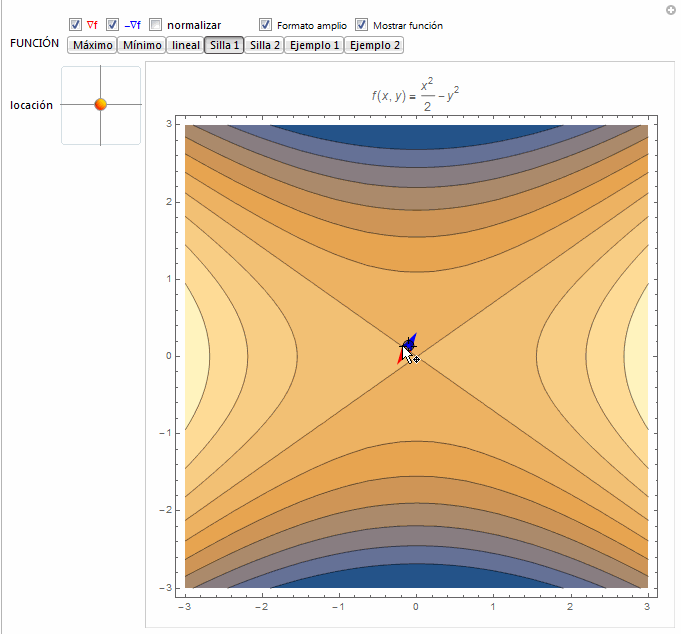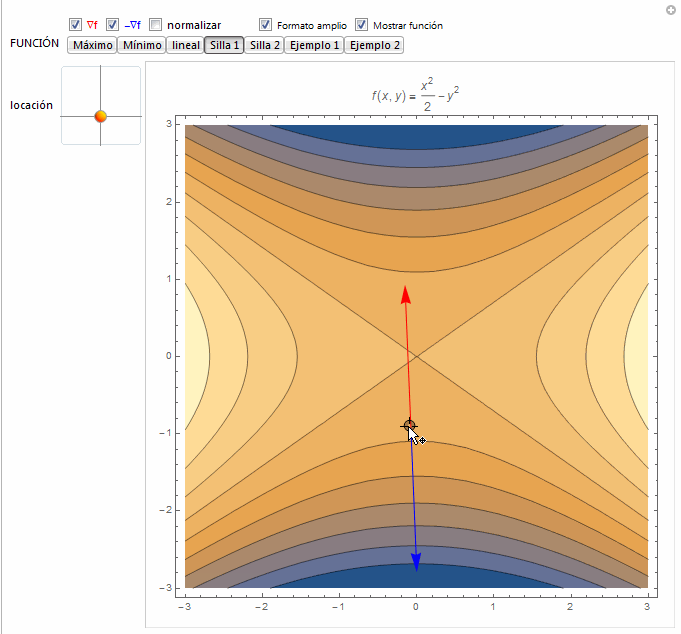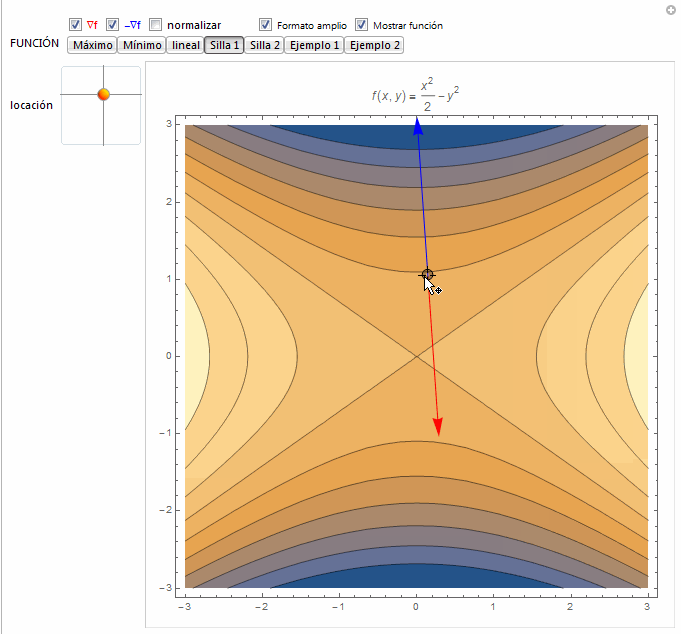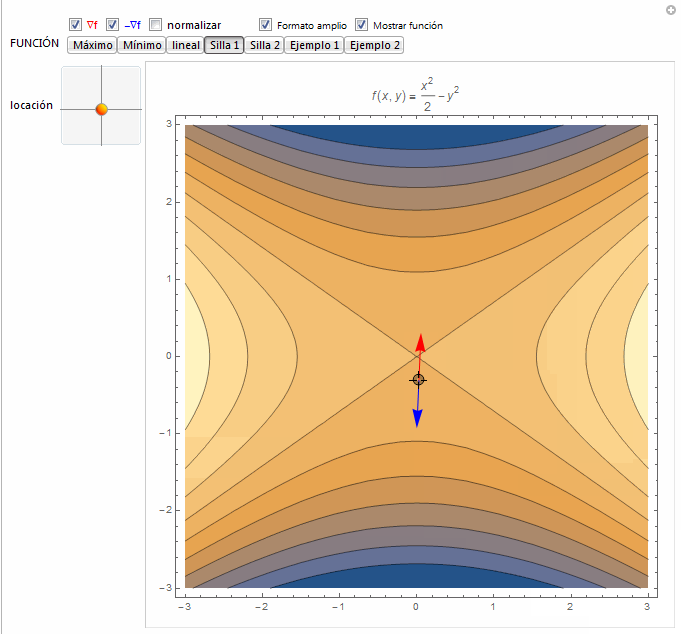
  function[x_, y_] := {5 - x^2/2 - y^2, x^2/2 + y^2, 1 - 2 x + y, 
    x^2/2 - y^2, -x^2/2 + y^2, Sin[Sin[y] + Sin[x]], 
    x y E^(-0.4 (x^2 + y^2))};
  buttonText = {" maximum", " minimum", " linear", " laddle 1", 
    " saddle 2", " example 1", " example 2"};
  functionButtons = 
   Map[#[[1]] -> #[[2]] &, 
    Transpose[{Range[Length[buttonText]], buttonText}]];
  grad = D[function[x, y][[fff]], {{x, y}}];
  unitgrad = grad/Sqrt[grad.grad]; 
  Deploy[
   Show[{
     ContourPlot[function[x, y][[fff]], {x, -3, 3}, {y, -3, 3}, 
      Contours -> 10],
     Graphics[{
       Red,
       If[MemberQ[options, gradient],
        If[
         MemberQ[options, normalize] && 
          Dynamic[grad /. {x -> pt[[1]], y -> pt[[2]]}] =!= {0, 0},
         Dynamic[
          Arrow[{pt, 
            pt + (unitgrad /. {x -> pt[[1]], y -> pt[[2]]})}]],
         Dynamic[Tooltip[
           Arrow[{pt, pt + (grad /. {x -> pt[[1]], y -> pt[[2]]})}], 
           Style[grad /. {x -> pt[[1]], y -> pt[[2]]}, Red]]],
         ],
        Red],
       If[
        MemberQ[options, normalize], {Black, Dynamic[Circle[pt, 1]]}, 
        Blue],
       Blue,
       If[MemberQ[options, neggradient],
        If[
         MemberQ[options, normalize] && 
          Dynamic[grad /. {x -> pt[[1]], y -> pt[[2]]}] =!= {0, 0}, 
         Dynamic[Arrow[{pt, 
            pt - (unitgrad /. {x -> pt[[1]], y -> pt[[2]]})}]],
         Dynamic[
          Tooltip[Arrow[{pt, 
             pt - (grad /. {x -> pt[[1]], y -> pt[[2]]})}], 
           Style[-grad /. {x -> pt[[1]], y -> pt[[2]]}, Blue]]]
         ],
        Blue],
       Tooltip[Locator[Dynamic[pt]], Dynamic[pt]]}]},
    ImageSize -> If[MemberQ[options, format], 500, 380],
    PlotLabel -> 
     If[MemberQ[options, label], 
      ToString[f[x, y], TraditionalForm] <> " = " <> 
       ToString[function[x, y][[fff]], TraditionalForm], 
      Column[{" "}, ItemSize -> {Automatic, 2.75}]]]]
  ],
 {{options, {gradient}, ""},
  {gradient -> Style[" \[Del]f", Red], 
   neggradient -> Style[" -\[Del]f", Blue], 
   normalize -> " normalizar          ", 
   format -> Style[" Formato amplio", 10],
   label -> Style[" Mostrar función", 10]}},
 {{fff, 1, "FUNCIÓN"}, functionButtons, ControlType -> Setter},
 {{pt, {1, 0}, "locación"}, {-3, -3}, {3, 3}, 
  ImageSize -> If[MemberQ[options, format], Medium, Tiny]},
 ControlType -> {CheckboxBar, Setter, Slider2D},
 ControlPlacement -> {Top, Top, Left},
 Initialization :> {Clear[x, y];
   buttonText = {" Máximo", " Mínimo", " lineal", " Silla 1", 
     " Silla 2", " Ejemplo 1", " Ejemplo 2"};
   functionButtons = 
    Map[#[[1]] -> #[[2]] &, 
     Transpose[{Range[Length[buttonText]], buttonText}]];}, 
 AutorunSequencing -> {1, 2, 3}]