=======================================================

Manipulate[
 x0 = pt[[1]]; y0 = pt[[2]];
 Show[
  Plot3D[f[x, y], {x, 0, 5}, {y, 0, 5}, MaxRecursion -> 2, 
   Ticks -> None, PlotRange -> {{0, 5}, {0, 5}, {0, 4}}, 
   SphericalRegion -> True, 
   AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, BoxRatios -> Automatic,
    Mesh -> False, PlotStyle -> Opacity[.6], BoundaryStyle -> None, 
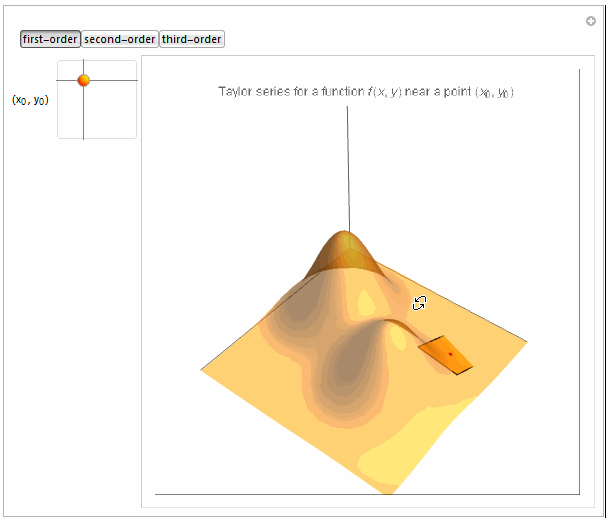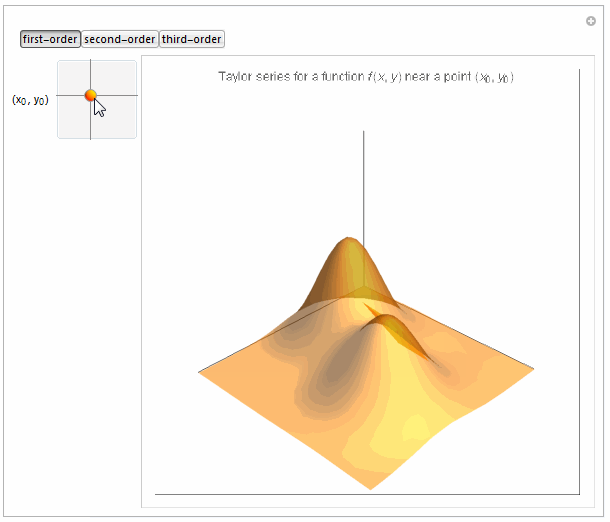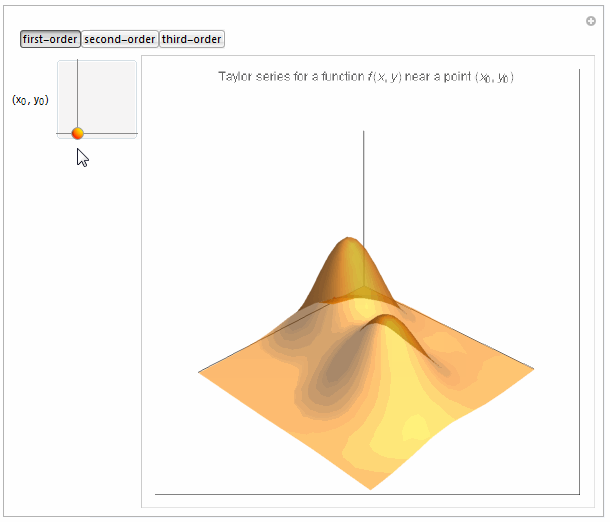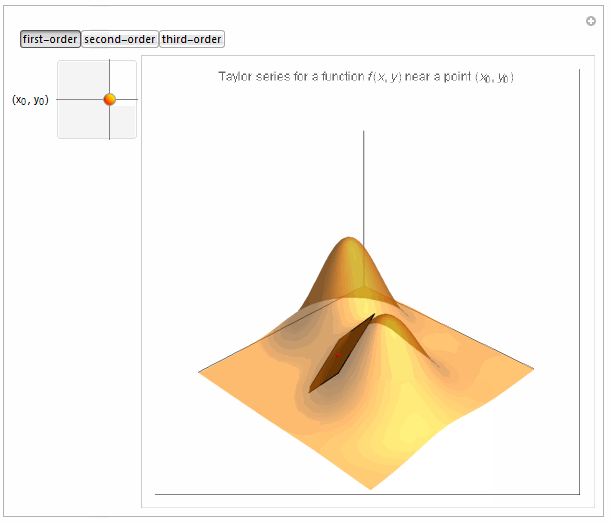
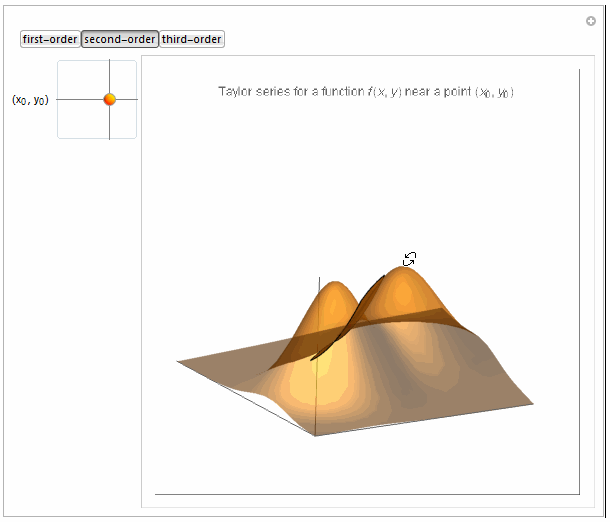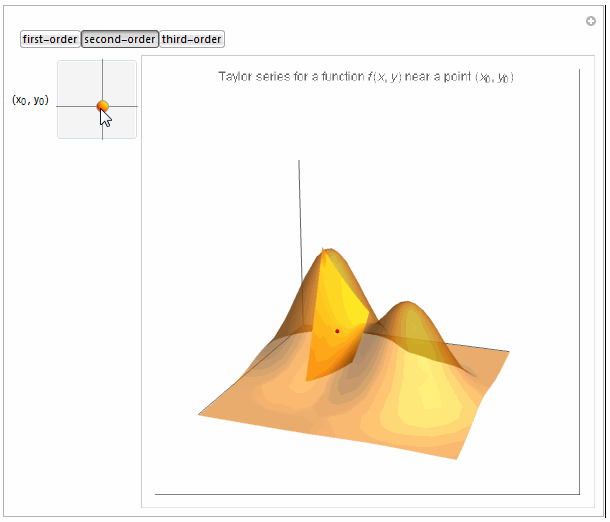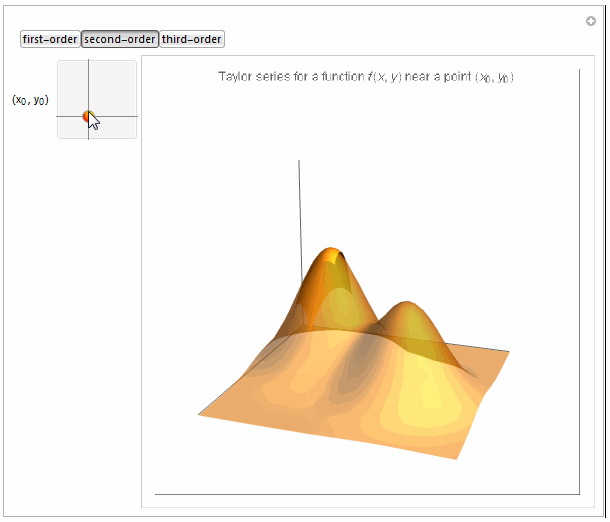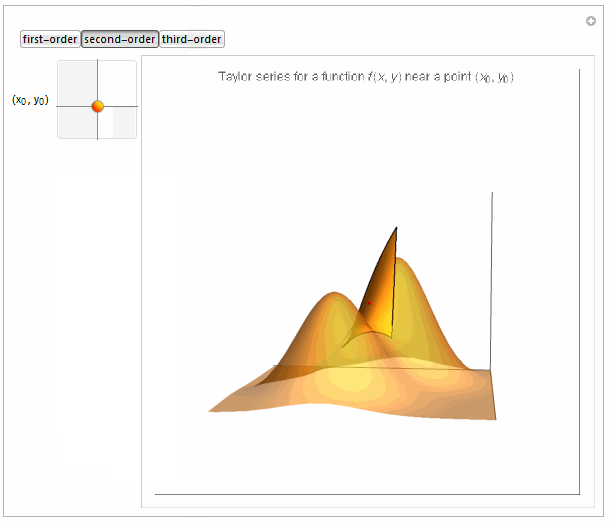
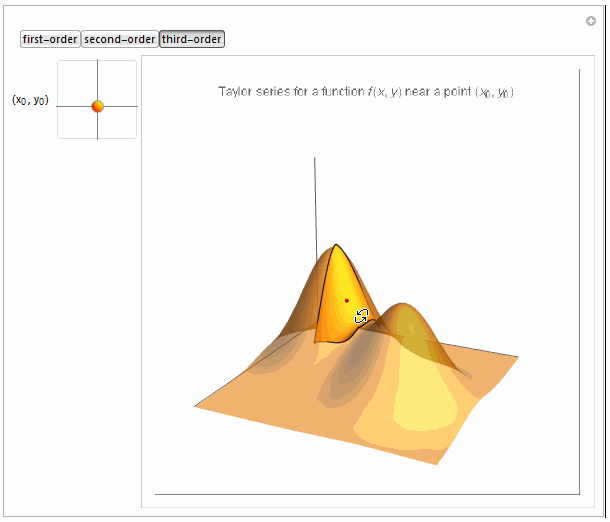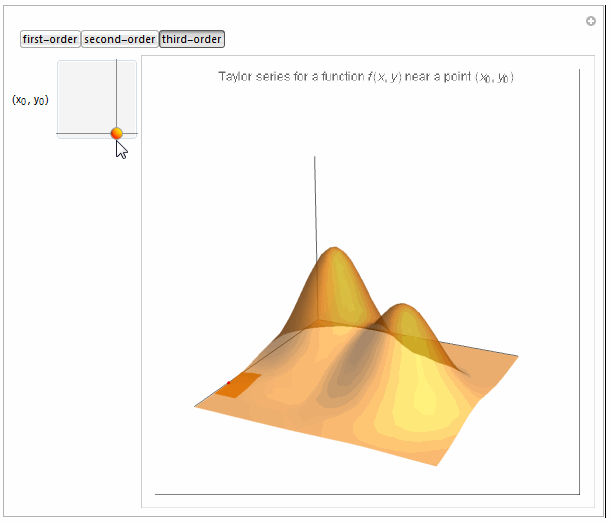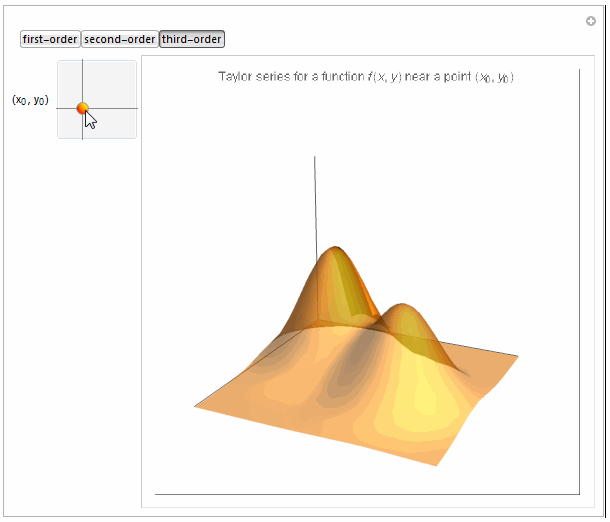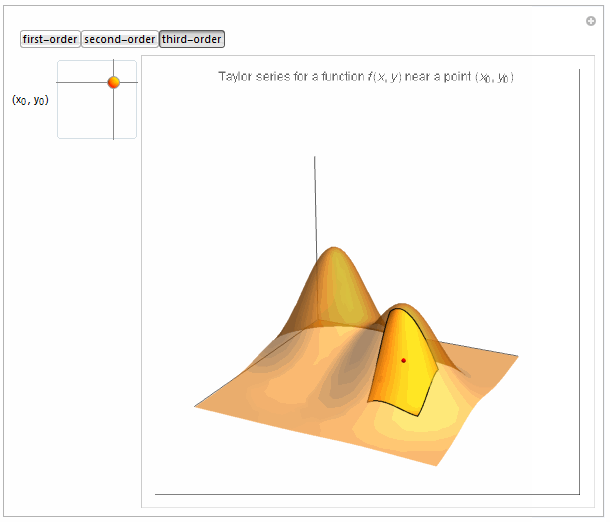
   Boxed -> False, PlotLabel -> Row[{
      "Taylor series for a function \!\(\*FormBox[\(f(x, y)\),
TraditionalForm]\) near a point \
\!\(\*FormBox[\((\*SubscriptBox[\(x\), \(0\)], \*SubscriptBox[\(y\), \
\(0\)])\),
TraditionalForm]\)"
      }]
   ],
  Graphics3D[{Red, Sphere[{x0, y0, f[x0, y0]}, .04]}],
  If[type == "first-order",
   Plot3D[
    f[x0, y0] + fx[x0, y0] (x - x0) + fy[x0, y0] (y - y0), {x, 
     x0 - len, x0 + len}, {y, y0 - len, y0 + len}, Mesh -> False, 
    PlotPoints -> 3],
   If[type == "second-order",
    Plot3D[
     f[x0, y0] + fx[x0, y0] (x - x0) + 
      fy[x0, y0] (y - y0) + .5 fxx[x0, y0] (x - x0)^2 + .5 fyy[x0, 
        y0] (y - y0)^2 + fxy[x0, y0] (x - x0) (y - y0), {x, x0 - len, 
      x0 + len}, {y, y0 - len, y0 + len}, Mesh -> False],
    Plot3D[
     f[x0, y0] + fx[x0, y0] (x - x0) + 
      fy[x0, y0] (y - y0) + .5 fxx[x0, y0] (x - x0)^2 + .5 fyy[x0, 
        y0] (y - y0)^2 + fxy[x0, y0] (x - x0) (y - y0)
      + (1/6)*(
        fxxx[x0, y0] (x - x0)^3
         + 3 fxxy[x0, y0] (x - x0)^2 (y - y0)
         + 3 fxyy[x0, y0] (x - x0) (y - y0)^2
         + fyyy[x0, y0] (y - y0)^3
        ), {x, x0 - len, x0 + len}, {y, y0 - len, y0 + len}, 
     Mesh -> False]
    ]
   ], ImageSize -> {400, 400}
  ],
 {{pt, {2.565, 2.585}, 
   Row[{"(", Subscript["x", 0], ", ", Subscript["y", 0], ")"}]}, {0, 
   0}, {5, 5}},
 {{type, "first-order", ""}, {"first-order", "second-order", 
   "third-order"}},
 ControlPlacement -> {Left, Top}, SaveDefinitions -> True, 
 TrackedSymbols -> True]