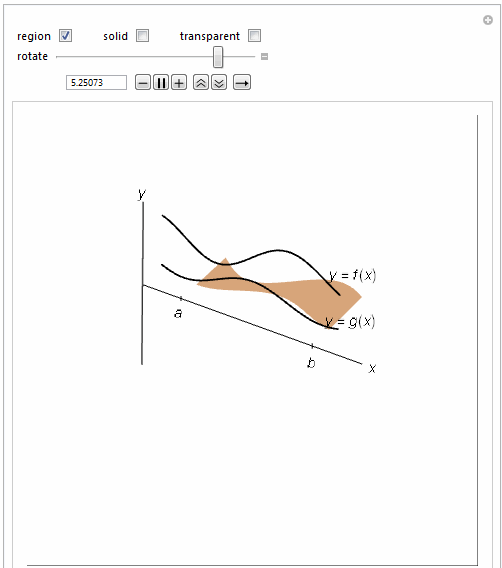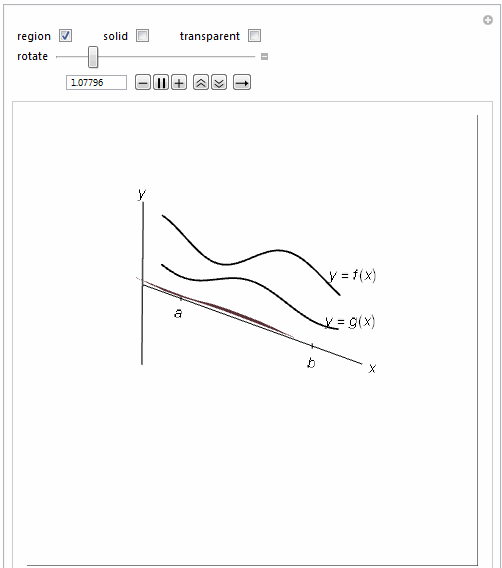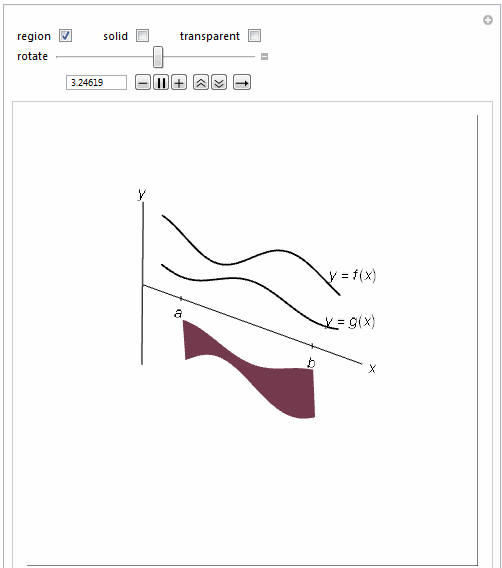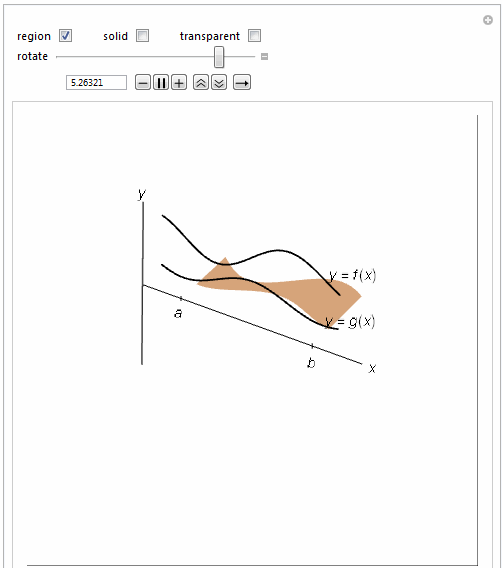
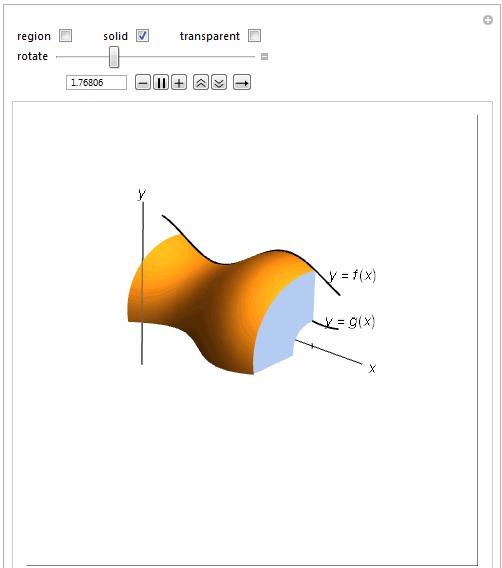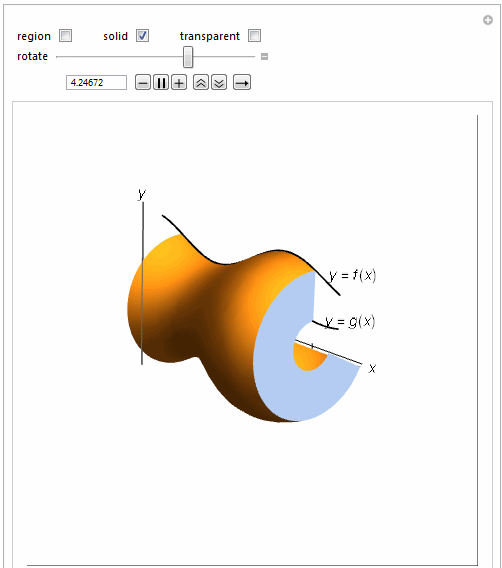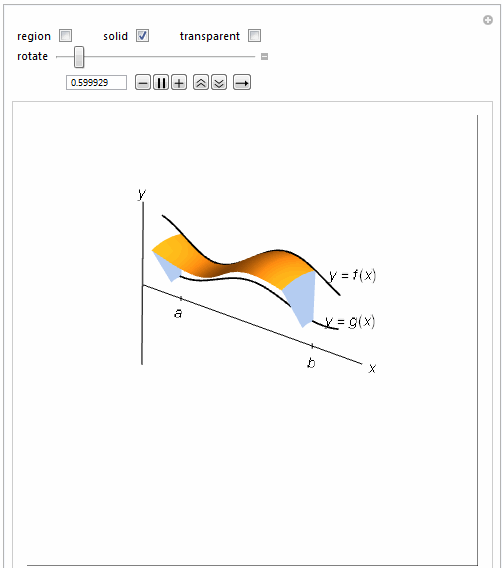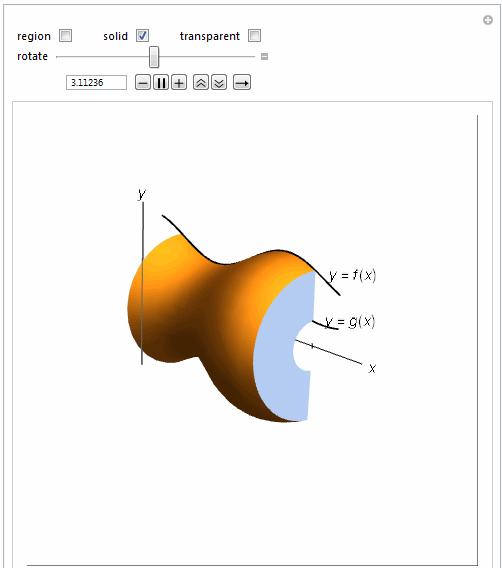
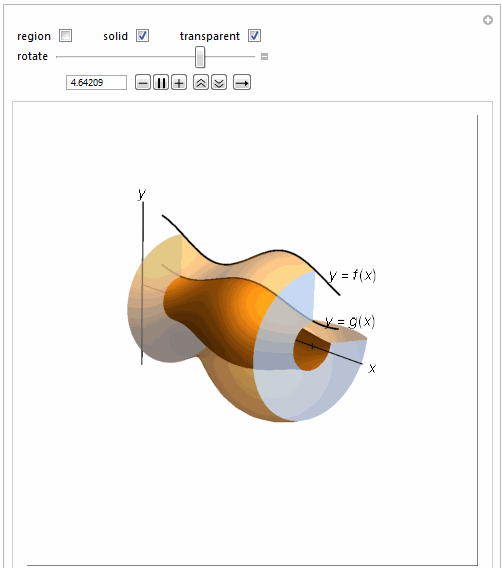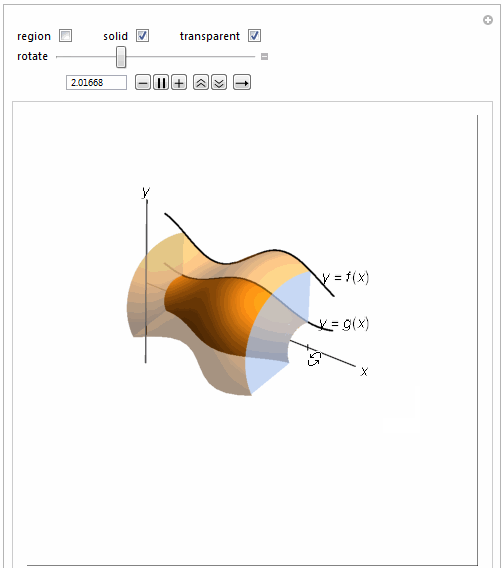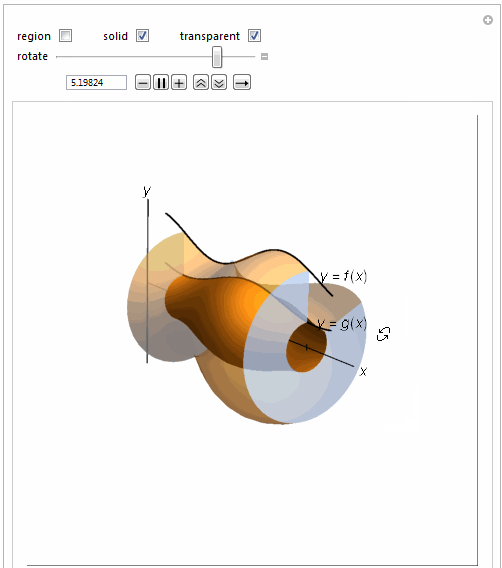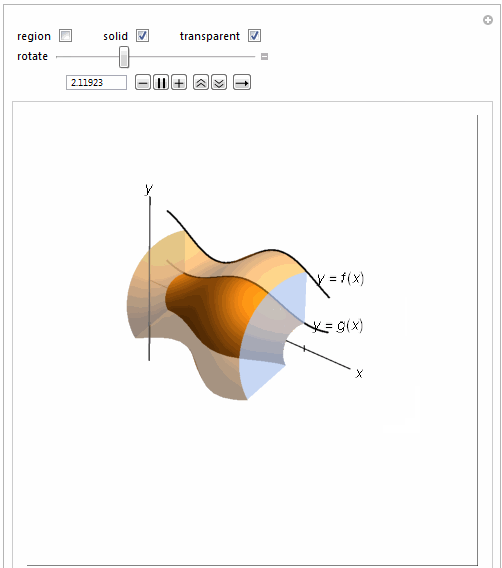
=============================================================

Manipulate[
 Show[{
   curverev1, curve2low,
   Graphics3D[
    {
     Line[{{1, 0, -.04}, {1, 0, .04}}],
     Line[{{4, 0, -.04}, {4, 0, .04}}],
     {Text[
       Row[{Style["y", Italic], " = ", Style["f", Italic], "(", 
         Style["x", Italic], ")"}], {4.75, 0, 1.2}],
      Text[
       Style[Row[{Style["y", Italic], " = ", Style["g", Italic], "(", 
          Style["x", Italic], ")"}], 14], {4.75, 0, .55}],
      If[\[Theta]1 < \[Pi]/2 || (Not[solidrev1] && \[Theta]1 > \[Pi]),
        Text[Style["a", Italic], {.95, 0, -.25}], {}],
      If[\[Theta]1 < \[Pi]/2 || (Not[solidrev1] && \[Theta]1 > \[Pi]),
        Text[Style["b", Italic], {4, 0, -.25}], {}],
      Text[Style["x", Italic], {5.2, 0, 0}],
      Text[Style["y", Italic], {0, 0, 1.5}]},
     {RGBColor[0, 0, 0], Line[{{0, 0, 0}, {5, 0, 0}}], 
      Line[{{0, 0, -4}, {0, 0, 4}}]},
     If[(regionrev1 && Not[solidrev1]) || (regionrev1 && 
         solidrev1 && \[Theta]1 < 2 \[Pi]), {EdgeForm[None], 
       LightBlue, 
       Polygon[Join[
         Table[{x, (.25 Sin[2 x + 1] + 
              1) Sin[-\[Theta]1], (.25 Sin[2 x + 1] + 
              1) Cos[-\[Theta]1]}, {x, 1, 4, .015}], 
         Table[{x, (.15 Cos[2 x + 1] + .5) Sin[-\[Theta]1], (.15 Cos[
                2 x + 1] + .5) Cos[-\[Theta]1]}, {x, 4, 
           1, -.015}]]]}, {}],
     If[solidrev1, {EdgeForm[None], 
       If[washtran, Opacity[.75], Opacity[1]], 
       Polygon[Join[
         Table[{4, (.25 Sin[9] + 1) Sin[-\[Theta]], (.25 Sin[9] + 
              1) Cos[-\[Theta]]}, {\[Theta], 
           0, \[Theta]1, \[Pi]/100}], 
         Table[{4, (.15 Cos[9] + .5) Sin[-\[Theta]], (.15 Cos[
                9] + .5) Cos[-\[Theta]]}, {\[Theta], \[Theta]1, 
           0, -\[Pi]/100}]]]}, {}],
     If[solidrev1, {EdgeForm[None], 
       If[washtran, Opacity[.75], Opacity[1]], 
       Polygon[Join[
         Table[{1, (.25 Sin[3] + 1) Sin[-\[Theta]], (.25 Sin[3] + 
              1) Cos[-\[Theta]]}, {\[Theta], 
           0, \[Theta]1, \[Pi]/100}], 
         Table[{1, (.15 Cos[3] + .5) Sin[-\[Theta]], (.15 Cos[
                3] + .5) Cos[-\[Theta]]}, {\[Theta], \[Theta]1, 
           0, -\[Pi]/100}]]]}, {}]
     }],
   If[solidrev1, 
    RevolutionPlot3D[.25 Sin[2 t + 1] + 1, {t, 1, 4}, {\[Theta], 
      0, \[Theta]1}, RevolutionAxis -> {1, 0, 0}, 
     PerformanceGoal -> "Quality", Mesh -> None, 
     PlotStyle -> If[washtran, Opacity[.5], Opacity[1]]], {}],
   If[solidrev1 && washtran, 
    RevolutionPlot3D[.15 Cos[2 t + 1] + .5, {t, 1, 4}, {\[Theta], 
      0, \[Theta]1}, RevolutionAxis -> {1, 0, 0}, 
     PerformanceGoal -> "Quality", Mesh -> None, 
     PlotStyle -> Opacity[1]], {}]
   }, PlotRange -> {{0, 5}, {-2, 2}, {-1.3, 1.3}},
  AxesOrigin -> {0, 0, 0}, Boxed -> False, 
  Axes -> {None, None, Automatic}, ViewPoint -> {1.5, -4, 0}, 
  Background -> White, ImageSize -> {450, 450}, 
  Ticks -> {{1, 4}, None, None}, BaseStyle -> 14]
 ,
 Delimiter,
 Grid[{{
    Control[{{regionrev1, True, "region"}, Checkbox}],
    Spacer[15],
    Control[{{solidrev1, True, "solid"}, Checkbox}],
    Spacer[15],
    Control[{{washtran, False, "transparent"}, Checkbox}],
    }}],
 {{\[Theta]1, \[Pi], "rotate"}, .0001, 2 \[Pi], 
  Enabled -> Dynamic[(regionrev1 || solidrev1)]},
 Initialization :> (curve2low = 
    ParametricPlot3D[{x, 0, .15 Cos[2 x + 1] + .5}, {x, .5, 4.5}, 
     PlotStyle -> {Black, AbsoluteThickness[1.75]}]; 
   curverev1 = 
    ParametricPlot3D[{x, 0, .25 Sin[2 x + 1] + 1}, {x, .5, 4.5}, 
     PlotStyle -> {Black, AbsoluteThickness[1.75]}]),
 SaveDefinitions -> True, AutorunSequencing -> {2, 4}]