=================================================================

Manipulate[Pane[
  
  Switch[fcns,
   reg1,
   f[x_] := 2 Sin[x] + 4;
   g[x_] := x/4,
   reg2,
   f[x_] := x^2/8 + 1;
   g[x_] := -x/4 + 1
   ];
  
  yrotate = -1;
  
  xmin = Pi/8;
  xmax = 2 Pi;
  
  ymax = 8;
  ymin = -ymax;
  
  $$viewangle = theview;  (* 1: Front, 2: Back *)
  viewlist = Part[{{0.5, 0.5, 1.5}, {0.5, 0.5, -1.5}}, $$viewangle];
  
  activestyle = {PlotPoints -> 16, MaxRecursion -> 0, Mesh -> False};
  
  inactivestyle = {PlotPoints -> 25, MaxRecursion -> 1, Mesh -> False,
     PlotStyle -> 
     If[MemberQ[plotopts, translucent], Opacity[0.5], Opacity[1]]};
  
  
  outsidesurface[thetamax_, opts___] := 
   ParametricPlot3D[{u, (f[u] - yrotate) Cos[v] + 
      yrotate, (f[u] - yrotate) Sin[v]}, {u, xmin, xmax}, {v, 0, 
     thetamax}, opts];
  
  insidesurface[thetamax_, opts___] := 
   ParametricPlot3D[{u, (g[u] - yrotate) Cos[v] + 
      yrotate, (g[u] - yrotate) Sin[v]}, {u, xmin, xmax}, {v, 0, 
     thetamax}, opts];
  
  a = xmin; b = xmax;
  endmin[thetamax_, opts___] := 
   If[Min[f[a] - yrotate, g[a] - yrotate] == 
     Max[f[a] - yrotate, g[a] - yrotate], {},
          
    ParametricPlot3D[{a, r Cos[t] + yrotate, r  Sin[t]}, {r, 
      Min[f[a] - yrotate, g[a] - yrotate],
                Max[f[a] - yrotate, g[a] - yrotate]}, {t, 0, 
      thetamax}, opts]];
  endmax[thetamax_, opts___] := 
   If[Min[f[b] - yrotate, g[b] - yrotate] == 
     Max[f[b] - yrotate, g[b] - yrotate], {},
          
    ParametricPlot3D[{b, r Cos[t] + yrotate, r  Sin[t]}, {r, 
      Min[f[b] - yrotate, g[b] - yrotate],
                Max[f[b] - yrotate, g[b] - yrotate]}, {t, 0, 
      thetamax}, opts]];
  
  startregion[opts___] := 
   ParametricPlot3D[{x, ((g[x] - f[x]) t + f[x]), 0}, {x, xmin, 
     xmax}, {t, 0, 1}, opts];
  
  (* Rotating Region *)
  rotatingregion[thetamax_, opts___] := Module[{},
    startlist = {x, ((g[x] - f[x]) t + f[x]) - yrotate, 0};
    rotmatrix = {{1, 0, 0}, {0, Cos[thetamax], -Sin[thetamax]}, {0, 
       Sin[thetamax], Cos[thetamax]}};
    plotlist = rotmatrix.startlist;
    
    region = 
     ParametricPlot3D[{plotlist[[1]], plotlist[[2]] + yrotate, 
       plotlist[[3]]}, {x, xmin, xmax}, {t, 0, 1}, opts]
    ];
  
  ThreeAxes = 
   ParametricPlot3D[{{xmax*t + xmin/2 (1 - t), 0, 0}, {0, 
      ymax/2*t + ymin/2 (1 - t), 0}, {0, 0, 
      ymax/2*t + ymin/2 (1 - t)}}, {t, 0, 1}, PlotStyle -> Black];
  
  revaxis = 
   ParametricPlot3D[{t, yrotate, 0}, {t, xmin, xmax}, 
    PlotStyle -> Red];
  
  
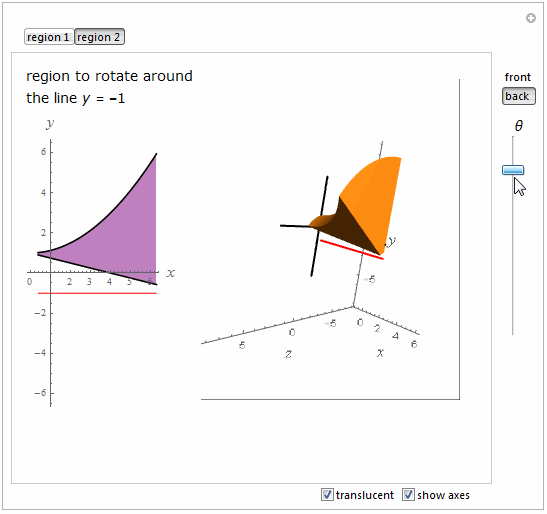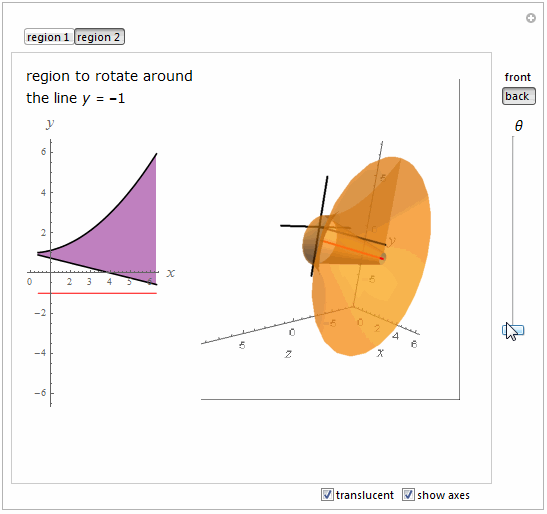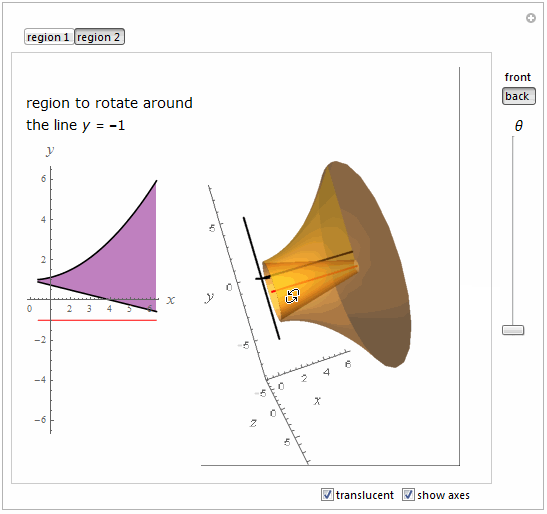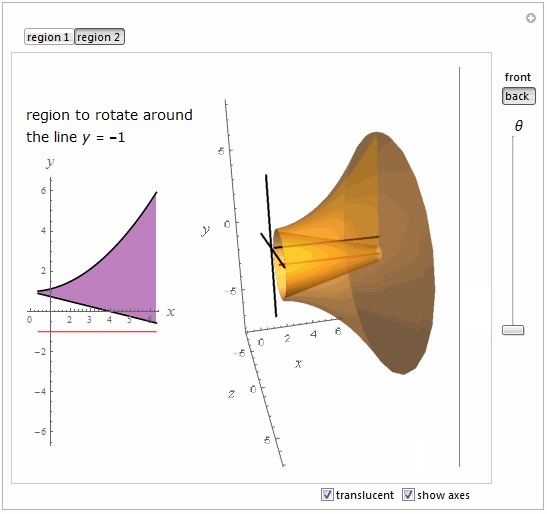
  regionplot = Show[
    Plot[{f[x], g[x]}, {x, a, b}, PlotStyle -> Black, Filling -> True,
      FillingStyle -> Lighter[Purple, 0.5]],
    Graphics[{Red, Line[{{a, yrotate}, {b, yrotate}}]}],
    AspectRatio -> Automatic, ImageSize -> 150,  
    AxesLabel -> {Text@Style["x", 16, Italic], 
      Text@Style["y", 16, Italic]}, PlotRange -> {-6, 6}];
  
  
  Grid[{{
     Deploy[
      Column[{Text@Style["region to rotate around", "Label", 14], 
        Text@Style[Row[{"the line ", Style[y, Italic], " = -1"}], 
          "Label", 14],
        regionplot
        }]],
     
     Show[
      If[th == 
        0, {}, {outsidesurface[th, 
         ControlActive[activestyle, inactivestyle]], 
        insidesurface[th, ControlActive[activestyle, inactivestyle]],
        endmin[th, ControlActive[activestyle, inactivestyle]],
        endmax[th, ControlActive[activestyle, inactivestyle]]}],
      startregion[ControlActive[activestyle, inactivestyle]],
      rotatingregion[th, ControlActive[activestyle, inactivestyle]],
      If[MemberQ[plotopts, showaxes], {ThreeAxes, revaxis}, {}], 
      Axes -> MemberQ[plotopts, showaxes],
      PlotRange -> {{-1, xmax}, {ymin, ymax}, {ymin, ymax}}, 
      Boxed -> False, AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, 
      ViewVertical -> {0, 1, 0}, ViewPoint -> viewlist, 
      AxesLabel -> {Text@Style["x", 16, Italic], 
        Text@Style["y", 16, Italic], Text@Style["z", 16, Italic]}, 
      ImageSize -> 258]
     }}], ImageSize -> {450, 400}],
 
 {{fcns, reg1, ""}, {reg1 -> "region 1", reg2 -> "region 2"}, 
  ControlPlacement -> Top},
 {{plotopts, {translucent, showaxes}, Spacer[295]}, {translucent, 
   showaxes -> "show axes"}, ControlPlacement -> Bottom, 
  ControlType -> CheckboxBar},
 "",
 {{theview, 1, ""}, {1 -> "front", 2 -> "back"}, 
  ControlPlacement -> Right, Appearance -> "Vertical"},
 "",
 Style["     \[Theta]", 14],
 {{th, 0, ""}, 2 Pi, 0, ControlType -> VerticalSlider, 
  ControlPlacement -> Right},
 ControlPlacement -> Right,
 
 TrackedSymbols :> {th, plotopts, theview, fcns}, 
 AutorunSequencing -> {3, 4}]