================================================================

Manipulate[
 
 Switch[views,
  
  uno, Pane[Grid[{
     {Text@
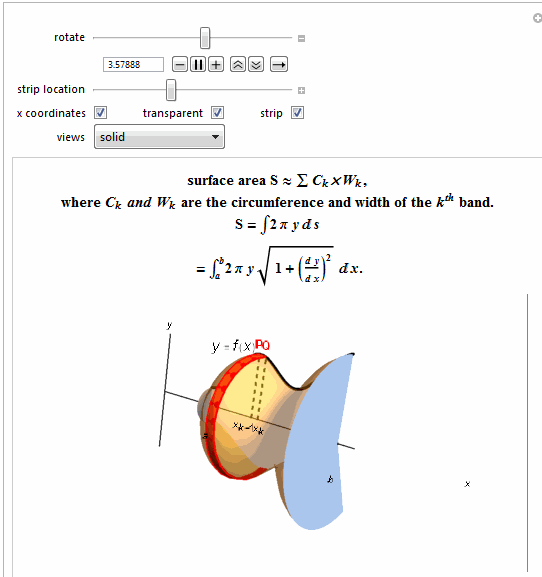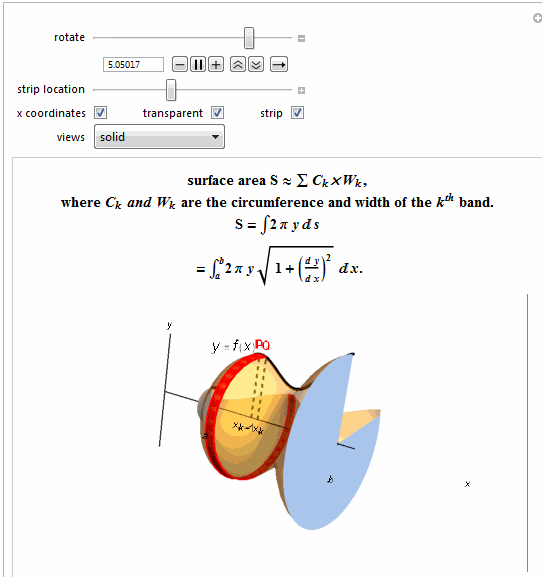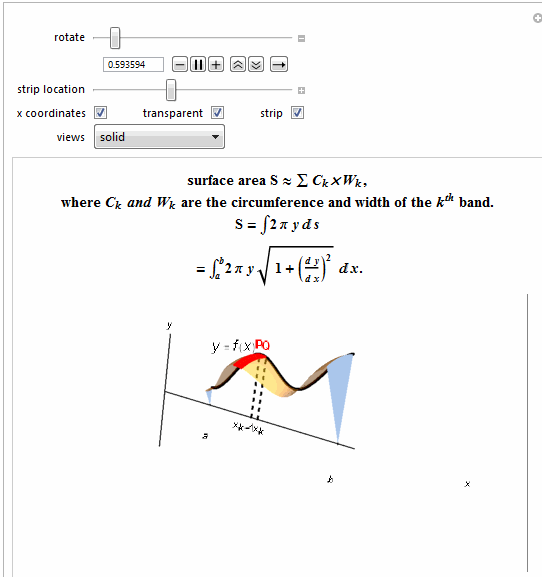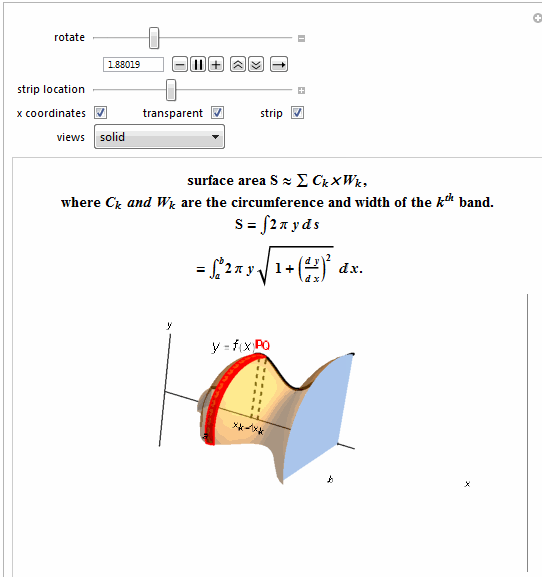
       Row[{"surface area S \[TildeTilde] \[Sum] ", 
         Style["\!\(\*SubscriptBox[\(C\), \
\(k\)]\)\[Times]\!\(\*SubscriptBox[\(W\), \(k\)]\)", Italic], ","}, 
        BaseStyle -> {Bold, 15}]},
     {Text@
       Row[{"where ", 
         Style["\!\(\*SubscriptBox[\(C\), \(k\)]\) and \
\!\(\*SubscriptBox[\(W\), \(k\)]\)", Italic], 
         " are the circumference and width of the ", 
         Style["\!\(\*SuperscriptBox[\(k\), \(th\)]\)", Italic], 
         " band."}, BaseStyle -> {Bold, 15}]},
     {Text@
       Row[{ "S = ", 
         TraditionalForm@
          HoldForm[\[Integral]2 \[Pi] y \[DifferentialD] s]}, 
        BaseStyle -> {Bold, 14}]},
     {Text@Row[{" = ", TraditionalForm@HoldForm[\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(a\), \(b\)]\(2  \[Pi]\ y 
\*SqrtBox[\(1 + 
\*SuperscriptBox[\((
\*FractionBox[\(d y\), \(d x\)])\), \(2\)]\)] \[DifferentialD]\ 
              x\)\)], "."}, BaseStyle -> {Bold, 14}]},
     {Show[{movable = True; rotatable = True; clickable = True; 
        selectable = False;
        If[xcoord && strip, Graphics3D[{
           {Dashed, Thick, 
            Line[{{aa, 0, 0}, {aa, 0, Sqrt[aa] + Sin[aa]}}]},
           {Dashed, Thick, 
            Line[{{aa + 0.5, 0, 0}, {aa + 0.5, 0, 
               Sqrt[aa + 0.5] + Sin[aa + 0.5]}}]},
           
           Text[Style[TraditionalForm@Subscript[x, k - 1], 
             Bold], {aa - 0.4, 0, -.5}],
           
           Text[Style["\!\(\*SubscriptBox[\(x\), \(k\)]\)", Bold, 
             Italic], {aa + 0.8, 0, -.5}],
           
           Text[Style["P", 12, Bold, Red], {aa, 0, 
             Sqrt[aa] + Sin[aa] + .6}],
           
           Text[Style["Q", 12, Bold, Red], {aa + 0.5, 0, 
             Sqrt[aa + 0.5] + Sin[aa + 0.5] + .7}]
           }], {}],
        Graphics3D
         [{
          {EdgeForm[None], 
           Polygon[
            Prepend[
             Table[{4.5, (Sqrt[4.5] + 
                  Sin[4.5]) Sin[-\[Theta]], (Sqrt[4.5] + 
                  Sin[4.5]) Cos[-\[Theta]]}, {\[Theta], 
               0, \[Theta]n, \[Pi]/36}], {4.5, 0, 0}]]},
          {EdgeForm[None], 
           Polygon[
            Prepend[
             Table[{14, (Sqrt[14] + 
                  Sin[14]) Sin[-\[Theta]], (Sqrt[14] + 
                  Sin[14]) Cos[-\[Theta]]}, {\[Theta], 
               0, \[Theta]n, \[Pi]/36}], {14, 0, 0}]]}
          }, BaseStyle -> If[trans, Opacity[0.5], Opacity[.9]]],
        curve, axis,
        If[strip, 
         RevolutionPlot3D[
          Sqrt[x] + Sin[x], {x, aa, aa + 0.5}, {\[Theta], 
           0, \[Theta]n}, RevolutionAxis -> {1, 0, 0}, Mesh -> None, 
          BoundaryStyle -> Directive[Red, Thick], 
          PlotStyle -> {Opacity[1], Red}, 
          PerformanceGoal -> "Quality"], {}],
        RevolutionPlot3D[
         Sqrt[x] + Sin[x], {x, 4.5, 14}, {\[Theta], 0, \[Theta]n}, 
         RevolutionAxis -> {1, 0, 0}, Mesh -> None, 
         PlotStyle -> If[trans, Opacity[0.5], Opacity[0.9]], 
         PerformanceGoal -> "Quality"]}, Boxed -> False, 
       ViewPoint -> Front, ImageSize -> {500, 300}, 
       PlotRange -> {{0, 15}, {-6, 6}, {-6, 6}}]}
     }], {500, 400}
   ],
  
  dos, Pane[Grid[{
     {Text@
       TraditionalForm@
        Row[{"circumference of a circle = ", 2 \[Pi] y, 
          " \[TildeTilde] ", 2 \[Pi], 
          HoldForm[(f[Subscript[x, k - 1]] + f[Subscript[x, k]])/(
           "2")]}, BaseStyle -> {Bold, 14}]},
     {Show[{graphics1, movable = False; clickable = False; 
        rotatable = True;
        RevolutionPlot3D[Sqrt[x], {x, 1, 3}, {\[Theta], 0, \[Theta]n},
          RevolutionAxis -> {1, 0, 0}, Mesh -> None, 
         PlotStyle -> If[trans, Opacity[0.5], Opacity[0.9]], 
         Axes -> False, PerformanceGoal -> "Quality"],
        If[xcoord, Graphics3D[{
           {Dashed, Thick, Red, Line[{{1, 0, 0}, {1, 0, 1}}]},
           {Dashed, Thick, Red, Line[{{3, 0, 0}, {3, 0, Sqrt[3]}}]},
           Text["\!\(\*SubscriptBox[\(x\), \(k - 1\)]\)", {1, 0, -.5}],
           
           Text["\!\(\*SubscriptBox[\(x\), \(k\)]\)", {3, 
             0, -.5}]}], {}]
        }, Boxed -> False, ViewPoint -> Front, 
       ImageSize -> {500, 300}, 
       PlotRange -> {{0, 4}, {-3, 3}, {-3, 3}}]}
     
     }], {500, 400}
   ],
  
  tres, Pane[Grid[{
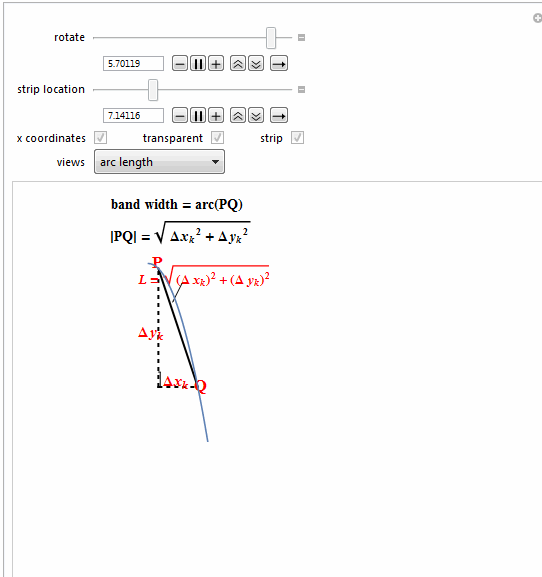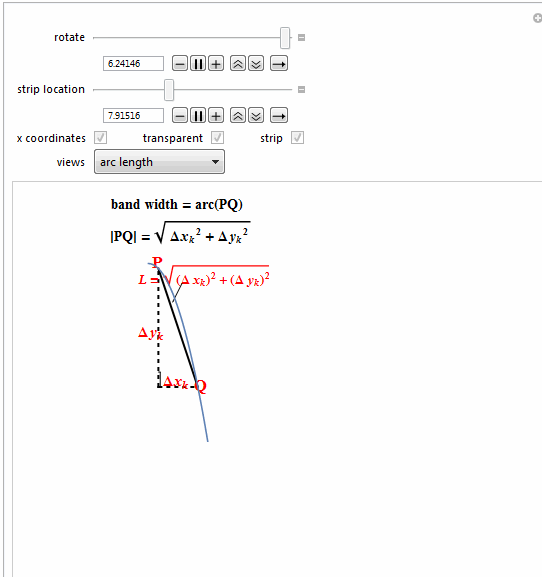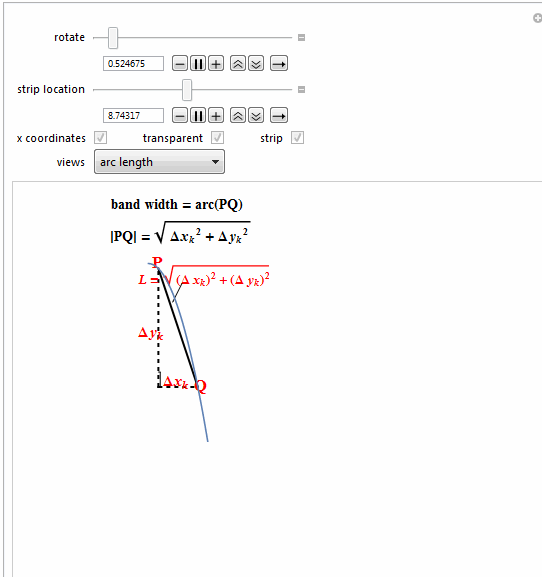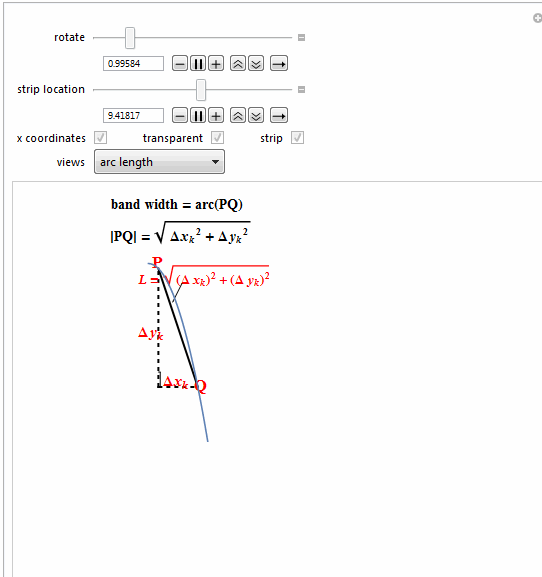
     {Text@Row[{"band width = arc(PQ)"}, BaseStyle -> {Bold, 14}]},
     {Text@
       Style[Row[{"  |PQ| = ", 
          Sqrt[Superscript[
             Subscript[Row[{"\[CapitalDelta]", Style["x", Italic]}], 
              Style["k", Italic]], 2] + 
            Superscript[
             Subscript[Row[{"\[CapitalDelta]", Style["y", Italic]}], 
              Style["k", Italic]], 2]]}], Bold, 14]},
     {Show[{movable = False; rotatable = False; selectable = True; 
        clickable = False; graphics2, 
        Plot[(-(x^2) + 10), {x, 0, 3}, 
         PlotRange -> {{0, 3.5}, {0, 12}}, Axes -> False]
        }, ImageSize -> {300, 200}, 
       ImagePadding -> {{60, 60}, {10, 10}}]}
     }, Alignment -> Center], {500, 400}]
  ],
 
 {{\[Theta]n, \[Pi], "rotate"}, 0.001, 2 \[Pi], 
  Enabled -> Dynamic[rotatable]},
 {{aa, 8, "strip location"}, 4.5, 13.5, 
  Enabled -> Dynamic[strip && movable]},
 Grid[{{
    Control[{{xcoord, True, "x coordinates"}, Checkbox, 
      Enabled -> Dynamic[strip && Not[selectable]]}], Spacer[20],
    Control[{{trans, True, "transparent"}, Checkbox, 
      Enabled -> Dynamic[strip && Not[selectable]]}], Spacer[20],
    Control[{{strip, True, "strip"}, Checkbox, 
      Enabled -> Dynamic[clickable]}]
    }}],
 {{views, uno, "views"}, {uno -> "solid", dos -> "frustrum of a cone",
    tres -> "arc length"}, ControlType -> PopupMenu},
 Initialization :> (
   curve = 
    ParametricPlot3D[{x, 0, Sqrt[x] + Sin[x]}, {x, 4.5, 14}, 
     PlotStyle -> {Black, AbsoluteThickness[3]}, Axes -> False, 
     Boxed -> False];
   curve2 = 
    ParametricPlot3D[{x, 0, Sqrt[x]}, {x, 1, 3}, 
     PlotStyle -> {Black, AbsoluteThickness[3]}, Axes -> False, 
     Boxed -> False];
   axis = Graphics3D[{Line[{{0, 0, 0}, {20, 0, 0}}],
      Line[{{0, 0, -4}, {0, 0, 4}}],
      Line[{{4.5, 0, -.05}, {4.5, 0, .05}}],
      Line[{{14, 0, -.05}, {14, 0, .05}}],
      Text[Style["a", Italic], {4.5, 0, -2}],
      Text[Style["b", Italic], {14, 0, -2}],
      Text[Style["x", Italic], {20.7, 0, 0}],
      Text[Style["y", Italic], {0, 0, 4.7}],
      Text[
       Row[{Style["y", 15, Italic], " = ", Style["f", 15, Italic], 
         "(", Style["x", 15, Italic], ")"}], {6, 0, 4}]}];
   graphics1 = Graphics3D[{
      Text[Style["x", Italic], {5.3, 0, 0}],
      Line[{{0, 0, 0}, {5, 0, 0}}],
      {Dashed, Thick, Line[{{2, 0, 0}, {2, 0, Sqrt[2]}}]},
      Text[Style["P", 12, Bold, Red], {1, 0, 1.5}],
      Text[Style["Q", 12, Bold, Red], {3, 0, Sqrt[3] + .4}],
      Text[Style["y", 15, Bold, Italic, Red], {2.3, 0, .5}],
      Text[Row[{"\[CapitalDelta]", Style["x", Italic]}], {2, 0, 2}],
      Polygon[
       Prepend[Table[{2, (Sqrt[2]) Sin[-\[Theta]], (Sqrt[
             2]) Cos[-\[Theta]]}, {\[Theta], 0, 2 \[Pi], \[Pi]/
          36}], {2, 0, 0}]]
      }, BaseStyle -> Bold];
   graphics2 = Graphics[{
      {Dashed, Thick, Line[{{0.5, 3.75}, {0.5, 39/4}}]},
      {Dashed, Thick, Line[{{0.5, 3.75}, {2.5, 3.75}}]},
      {Thick, Line[{{0.5, 39/4}, {2.5, 3.75}}]},
      Line[{{0.5, 4.5}, {0.6, 4.5}}],
      Line[{{0.6, 3.75}, {0.6, 4.5}}],
      Text[Style["P", 17, Bold, Red], {0.5, 10.0}],
      Text[Style["Q", 17, Bold, Red], {2.67, 3.75}],
      Text[
       Style[TraditionalForm@
         Row[{L, " = ", 
           HoldForm[ 
            Sqrt[(\[CapitalDelta] Subscript[x, 
               k])^2 + (\[CapitalDelta] Subscript[y, k])^2]]}], 13, 
        Bold, Red], {3, 9.3}],
      Text[
       Style[Row[{\[CapitalDelta], Subscript[x, k]}], 15, Bold, 
        Red], {1.5, 4}],
      Text[
       Style[Row[{\[CapitalDelta], Subscript[y, k]}], 15, Bold, 
        Red], {0.2, 6.5}],
      Arrow[{{1.7, 9}, {1.2, 8}}]
      }, BaseStyle -> Bold]
   )]